Cet article est une quête annexe du tuto général pour ASP, s'intéressant à la modélisation et résolution de problème de logique, sous la forme d'une volée de cas pratiques.

les sources des codes peuvent être trouvés sur mon dépôt learning-ASP,

Les premiers problèmes sont les warmup logic exercises du site brilliant.org. Tous les problèmes ne sont pas solvables simplement, mais pour ceux qui le sont, cela permet de découper la méthode logique nécessaire à leur résolution.

Ensuite, s'intercale une partie sur les limites d'ASP, en montrant des énigmes qu'ASP ne peut pas résoudre directement, puis on ré-attaque différentes énigmes ou questions trouvées ça et là.

On terminera en trombe sur l'énigme d'Einstein, qui fait intervenir des nordiques fumant et buvant avec leurs animaux de compagnie dans des maisons colorées.

À la fin, on montrera même comment rendre l'énigme plus complexe.

Énigmes simples

Les énigmes qui suivent viennent du site brilliant.org. Les codes sont agglomérés ici.

brothers

On nous donne les tailles relatives de 5 frères (par exemple, Alex est plus grand que Brian), et nous devons deviner qui est le plus grand.

Nous avons les données suivantes :

plus_grand_que(alex,brian).
plus_grand_que(charlie,alex).
plus_grand_que(daniel,edward).
plus_grand_que(alex,daniel).

Comment résoudre le problème ? Une fois les données ainsi couchées, la méthodologie est évidente : les plus grands sont ceux qui ne sont jamais plus petits qu'un autre :

plus_grand(X):- plus_grand_que(X,_) ; not plus_grand_que(_,X).

En fait, il s'agit là d'un problème de recherche de racine d'un arbre. Nous avons un arbre, définit par les arcs «plus grand que», où la source d'un arc est plus grand que la cible, et nous cherchons celui qui n'a aucun prédécesseur, c'est-à-dire la racine.

C'est un problème assez standard de théorie des graphes, et la résolution est intuitive dés lors que l'on visualise l'arbre tel qu'il est réellement :

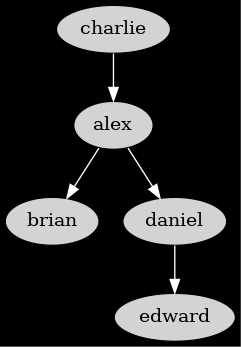
Questions

Soit deux questions :

1. Sont-ce «oui» et «non» des réponses invalides pour la question 2 ?
2. «oui» ou «non» est-il une réponse valide pour la question 1 ?

Question : quelle est la réponse à la question 2 ?

La méthode pour répondre à cette question peut consister à essayer toutes les combinaisons de oui et non, et voir si la proprosition est logique. Par exemple, Si je répond oui au deux questions, il y a un problème, car répondre oui à la question 1 implique qu'on ne peut pas répondre oui à la question 2. En essayant les quatre combinaisons, nous trouverions la bonne. En ASP, cela peut s'encoder ainsi :

% Si on répond «oui» à la question 1, c'est parce qu'on ne peut répondre ni oui ni non à la question 2.
q1(oui):- not q2(oui) ; not q2(non).
% Si on répond «oui» à la question 2, c'est parce qu'on répond «oui» ou «non» à la question 1.
q2(oui):- q1(oui;non).
% Si on ne répond pas oui à une des deux questions, on répond non.
q1(non):- not q1(oui).
q2(non):- not q2(oui).

Notez que les deux dernières lignes sont logiques, car les questions sont fermées, et nécessaires, car l'ordinateur ne peut pas le deviner tout seul. Le jour où des IA fortes nous assisterons dans notre création de code, ce genre de ligne sera automatiquement ajoutées par l'IA en question. Mais d'ici là, il nous faut y penser nous même.

Déclarations contradictoires

1. Il y a exactement 1 fausse déclaration dans cette liste.
2. Il y a exactement 2 fausses déclarations dans cette liste.
3. Il y a exactement 3 fausses déclarations dans cette liste.

Combien y a t-il de fausses déclarations dans cette liste ?

% De toute évidence, toutes les propositions sont exclusives, donc il ne peut y avoir qu'une seule de vraie, ou aucune.
0{p(1..3)}1.

Notez que si il y doit y avoir exactement une vraie déclaration, même sans ASP, écrire cette évidence nous donne presque la réponse. En effet, si une seule est vraie, alors 2 sont fausses. N'avoir aucune garantie de la véracité d'au moins une déclaration complexifie un peu le problème, à cause de la proposition 3 (qui induit un conflit).

Écrivons les déclarations, et voyons si ASP s'en sort :

% La première est vraie si une est fausse, donc si deux sont vraies.
p(1):- 2 { p(_) } 2.
% La seconde est vraie si deux sont fausses, donc si une seule est vraie.
p(2):- 1 { p(_) } 1.
% La troisième est vraie si les trois sont fausses.
p(3):- not p(_).

La réponse, unique, du solveur, est bien sûr p(2). En effet, si une proposition est vraie, il s'agit nécessairement de p(2), par définition. Si aucune n'est vraie, alors p(3) pourrait être valide… Sauf que dans un tel cas, la proposition n'est plus vraie. Par conséquent, il n'existe aucun modèle stable dans lequel p(3) serait valide.

Recherche de vérité

Premier

Énoncé

• Le chevalier dit toujours la vérité.
• La canaille ment toujours.
• Le joker peut faire les deux.

Question : L'un des trois dit «je suis une canaille». Qui est-il ?

Résolution

% C'est l'un des trois.
1 {chevalier ; canaille ; joker} 1.

% Que pourrais dirais chaque agent s'il parlait ?
reponse(chevalier):- chevalier.
reponse(chevalier) ; reponse(joker):- canaille.
reponse(chevalier) ; reponse(canaille) ; reponse(joker):- joker.

% On sait que l'agent à dit qu'il était la canaille, donc il doit être dans la réponse.
:- not reponse(canaille).

Écrire proprement le problème permet de trouver la réponse, même sans aller chercher clingo. Ici, on voit bien que parmis les atomes qui peuvent être générés, seul le joker peut dire reponse(canaille). Par conséquent, c'est le joker qui a parlé.

Second

Énoncé

• Le chevalier dit toujours la vérité.
• La canaille ment toujours.
• Le joker peut faire les deux.

Trois agents savent qui ils sont, et disent:

• ellis: farin est un joker
• farin: gobi est un joker
• gobi: ellis est un joker

Question: Sachant qu'il n'y a qu'un seul joker, combien y a-t-il de chevaliers ?

Résolution

% Données.
type(chevalier;canaille;joker).
agent(ellis;farin;gobi).

% Each one has a kind.
1 { type(P,K): type(K) } 1:- agent(P).

% There is one and only one joker.
1 { type(P,joker): agent(P) } 1.

% Nombre de chevalier.
reponse(N):- N={type(_,chevalier)}.

% Ce qu'un chevalier dit est vrai.
type(farin,joker):- type(ellis,chevalier).
type(gobi,joker):- type(farin,chevalier).
type(ellis,joker):- type(gobi,chevalier).

% Knaves can't tell the truth.
:- type(farin,joker) ; type(ellis,canaille).
:- type(gobi,joker) ; type(farin,canaille).
:- type(ellis,joker) ; type(gobi,canaille).

Les ensemble réponse indiquent tous la même chose : il y a un chevalier, une canaille et un joker. Comme les données sont symétriques, si l'on fixe l'un des trois agent comme chevalier, les autres voient leur rôle fixé. Par exemple, si ellis est chevalier, alors farin est un joker, ce qui pourrait impliquer que gobi en est un aussi, sauf que l'on sait qu'il n'y en a qu'un seul, donc, comme il ment, c'est une canaille.

Second, le retour en terre de chevaliers

Énoncé

Une variation du thème précédent n'employant que des chevaliers et des canailles est proposé ici.

L'énoncé est le suivant :

Sur une île, on ne trouve que 2 types d'habitants, les chevaliers (qui disent toujours la vérité) et les canailles (qui mentent toujours). Considérons trois habitants, A, B et C. A dit «B et C sont de même type» (ils sont soit deux chevalier, soit deux canailles). On demande ensuite à C si A et B sont de même type. Quelle est la réponse de C ?

Certaines des réponses données par les participants sont très intéressantes, notamment celle-ci. La résolution en ASP est quant à elle un poil longue.

Résolution

habitants(a;b;c).
1 { chevalier(X) ; canaille(X) } 1 :- habitants(X).

% A dit que B et C sont de même type.
idem(b,c) :- chevalier(a).
diff(b,c) :- canaille(a).

% Implementation de idem/2 et diff/2.
idem(X,Y) :- chevalier(X) ; chevalier(Y) ; X!=Y.
idem(X,Y) :- canaille(X) ; canaille(Y) ; X!=Y.
diff(X,Y) :- chevalier(X) ; canaille(Y) ; X!=Y.
diff(X,Y) :- diff(Y,X).
:- idem(X,Y) ; chevalier(X) ; canaille(Y).
:- idem(Y,X) ; chevalier(X) ; canaille(Y).
:- diff(X,Y) ; chevalier(X) ; chevalier(Y).
:- diff(Y,X) ; canaille(X) ; canaille(Y).

% Quelle est la réponse de C ?
reponse(yes) :- chevalier(c) ; idem(a,b).
reponse(yes) :- canaille(c) ; diff(a,b).
reponse(no) :- canaille(c) ; idem(a,b).
reponse(no) :- chevalier(c) ; diff(a,b).

#show reponse/1.

Troisième

Énoncé

Trois boîtes indiquent chacune :

1. la voiture est dans la boite 1.
2. la voiture n'est pas dans la boite 2.
3. la voiture n'est pas dans la boite 1.

Sachant qu'il n'y a qu'une voiture, et qu'une seule des boîte indique une vérité, où est la voiture ?

Résolution

1 { p(1;2;3) } 1.    % une seule proposition est vraie
1 { car(1;2;3) } 1.  % une seule voiture

% Si la voiture est dans la boîte 1, alors la boîte 1 dit vrai.
p(1):- car(1).
% Si la voiture n'est pas dans la boîte 2, alors la boîte 2 dit vrai.
p(2):- not car(2).
% 
p(3):- not car(1).

En écrivant ces règles, on devine immédiatement le problème. La réponse est car(2) p(3).

Limites d'ASP

La quatrième des énigmes proposées dans la catégorie «recherche de vérité» n'est pas facilement soluble avec ASP. Intéressons-nous à ce cas un peu particulier.

Quatrième

On a 4 boites. La première est étiquettée comme contenant une pomme, la seconde une banane, la troisième une carotte, et la dernière une datte. Sachant qu'une seule d'entre elle est étiquettée correctement, combien de boites au pire doit-on ouvrir pour savoir de laquelle il s'agit ?

Cette énigme ne se résouds pas en ASP, du moins pas de manière directe comme on a pu le faire jusqu'ici. La résolution de cette énigme requiert l'usage de la logique épistémique, où l'on est capable de représenter les connaissances de différents agents.

Résoudre avec une itérative

Une solution pour s'en dépatouiller est de faire l'algo nous-même. Déjà, on observe que lorsqu'on ouvre une boite, il y a deux cas de figure :

1. on ouvre la boite correctement étiquettée
2. on ouvre une autre boite

Le premier cas ne nous intéresse pas, car il ne répond pas à la question (qui demande le pire cas, i.e. quand on ouvre jamais la bonne boite). Le second, en revanche, nous donne deux informations. Mettons que l'on ouvre la boite 2, qui contient une carotte : nous pouvons dire que, évidemment, la boite 2 n'est pas correctement étiquettée, mais également que la boite trois, étiquettée comme contenant une carotte, n'est pas bien étiquettée non plus, puisque nous venons de trouver la carotte dans une autre boite.

Donc, en utilisant cette double détection de mauvaise étiquette, nous pouvons dire que les boites 2 et 3 sont mal étiquettées.

Maintenant, nous pouvons recommencer : ouvrir une autre boite que l'on a pas découverte mal étiquettée précédemment. Et ce, jusqu'à ce qu'il ne reste plus qu'une boite : il s'agit nécessairement de la boite bien étiquettée.

Algo et espace de recherche

Nous allons donc implémenter cet algo : ouvrir une (mauvaise) boite, décider lesquelles sont donc mal étiquettées, et recommencer jusqu'à n'avoir plus qu'une boite. La question étant de trouver le pire cas, il faudra donc chercher la solution qui maximise le nombre d'itérations.

Il y a différentes manière de donner la réponse, par exemple :

• donner, pour n'importe quelle répartition d'objets dans les boites, toutes les séquences possibles et leur sortie («a-t-on réussi à trouver la bonne boite ?»)
• donner, pour une répartition particulière d'objets, toutes les séquences possibles et leur sortie
• donner, pour une répartition particulière d'objets, les séquences qui permettent de connaître la bonne boite
• donner, pour une répartition particulière d'objets, les tailles des séquences qui permettent de connaître la bonne boite

(par séquence, on entend l'ordre dans lequel il faut ouvrir quelle boite ; la taille d'une séquence est donc le nombre de boite à ouvrir)

En modifiant légèrement le code ASP, nous pourrons avoir l'une ou l'autre des réponses. Celle qui répond effectivement à la question est bien sûr la dernière méthode : si il faut ouvrir 2 boites, on veut obtenir «2», rien de plus. La troisième méthode nous donnerais en plus les boites à ouvrir (la numéro 2, puis la 4).

Enfin, notons que l'espace de recherche possède quelques symmétries : par exemple, que la bonne boite soit la numéro 1, 2, 3 ou 4, cela ne changera pas la réponse, car il n'y au aucune différence entre résoudre le problème quand la bonne boite est la 2, ou quand elle est la 3. Nous allons donc pouvoir, dans notre encoding ASP, encoder une situation particulière. Par défaut, nous prendrons que la bonne boite est la 1, i.e. qu'elle contient une pomme (apple).

Bien que ce soit inutile, rien ne nous empêchera ensuite de formuler le code pour qu'il cherche la réponse parmi toutes les combinaisons boite/objet possible.

C'est parti !

L'encoding

Déjà, commençons par déclarer les étiquettes, et en déduire les raccourcis vers les boites et les objets :

label(1,apple).
label(2,banana).
label(3,carrot).
label(4,date).
item(I):- label(_,I).
box(B):- label(B,_).
nb_box(N):- N=#max{B:box(B)}.  % nombre maximal d'ouvertures nécessaires

Ensuite, choisissons un cas bien précis : la pomme est bien placé, les autres non :

contains(1,apple).  correct(1).
contains(2,carrot).
contains(3,date).
contains(4,banana).

Maintenant, commençons la partie iterative. D'abord, définissons que nous commençons au pas (step) zéro, et décidons quelle boite peuvent être ouvertes :

choosable(N,B):- step(N-1) ; box(B) ; not bad(N-1,B) ; not correct(B).

On utilise N comme le numéro de pas. Ici, on dit bien que la boite B peut être choisie à l'étape N si à l'étape précédente, elle n'était pas connue pour être mal étiquettée, et qu'il ne s'agit pas de la bonne boite (sinon c'est trop simple).

Maintenant, choisissons une boite à ouvrir :

step(0).  % le prochain step est donc le 1
0 { open(N,B): choosable(N,B) } 1 :- step(N-1) ; N<NbBox ; nb_box(NbBox).
step(N):- open(N,_).

Le nombre de boite est le numéro de pas maximal : l'autre solution pour éviter un grounding infini eût été de donner un grand nombre, genre 100. Mais c'est plus économique de juste dire qu'au maximum, on ouvre autant de boite qu'il y en a dans le problème posé (mois une, car même dans le pire cas on ouvre pas la dernière boite).

Maintenant, propageons la connaissance obtenue :

%  on se souvient des mauvais précédents:
bad(N,B):- step(N) ; bad(N-1,B).
%  la boite ouverte est mauvaise:
bad(N,B):- open(N,B) ; step(N).
%  et celle qui est étiquettée avec l'objet trouvé aussi:
bad(N,B):- open(N,O) ; step(N) ; contains(O,I) ; label(B,I).

Nous avons donc bad/2, qui nous indique pour un step donné ce que nous savons sur les boites, i.e. lesquelles sont mal étiquettées. Comme nous allons ouvrir des boites tant qu'il y en a de choosable, le solver va donc énumérer des modèles contenant des séquences d'ouvertures, jusqu'à ce qu'il n'y en ai plus. Cependant, comme la règle d'ouverture stipule que l'on peut choisir entre 0 et 1 boite à ouvrir, cela veut dire que le solveur peut tout à fait s'arrêter avant d'avoir trouvé toutes les mauvaises boites. D'où les lignes suivantes, où l'on écarte les modèles qui ne terminent pas le travail, c'est-à-dire ceux qui n'identifie pas toutes les boites sauf une comme mal étiquettées :

finished(B):- box(B) ; not bad(_,B) ; 1{box(X): not bad(_,X), box(X)}1.
:- not finished(_).  % on écarte le modèle s'il ne termine pas

Pour simplifier l'affichage, arrangeons-nous pour n'afficher que les ouvertures :

#show open/2.

Et, en lançant le solveur, nous obtenons… roulement de tambour

clingo version 5.2.2
Reading from l.lp
Solving...
Answer: 1
open(1,4) open(2,3)
Answer: 2
open(1,2) open(2,4)
Answer: 3
open(1,3) open(2,2)
SATISFIABLE

Models       : 3
Calls        : 1
Time         : 0.010s (Solving: 0.00s 1st Model: 0.00s Unsat: 0.00s)
CPU Time     : 0.010s

Trois possibilités, toutes de deux ouvertures. En affichant également les bad/2, on peut voir l'évolution de la connaissance au fur et à mesure. On découvre ainsi que, pour trouver la bonne boite, il suffit d'en ouvrir deux dans le pire cas. Voilà la réponse à la question.

Cependant, il y a encore bien des choses à dire…

Généralisations

Avez-vous remarqué que le code est spécifiquement fait pour pouvoir facilement rajouter des objets ? C'est parti, rajoutons des boites !

label(1,apple).
label(2,banana).
label(3,carrot).
label(4,date).
label(5,eggfruit).
label(6,fig).
label(7,grape).
label(8,huckleberry).

Et paf ! 936 modèles ! Effectivement, il manque les contains/2, qui ajoute de la variabilité malvenue. Ajoutons-les manuellement :

contains(5,fig).
contains(6,grape).
contains(7,huckleberry).
contains(8,eggfruit).

Et bim ! 192 modèles ! Bon, on va pas s'amuser à les détailler, mais en gros, vous pouvez par exemple ouvrir la 3, la 5, la 8, la 2 et enfin la 7, donnant donc la solution en 5 ouvertures. Ou encore ouvrir la 3, la 2, la 8 et la 6, donnant la solution en 4 ouvertures. Holà ! Intéressante découverte : il y des solutions de plusieurs tailles !

Énumérations des possibilités

Essayons d'étudier la question proprement : quelles sont les facteurs qui peuvent changer la taille de la solution ? Et bien, avec 5 boites, il y a déjà une variabilité ; on trouve 8 modèles allant de 2 à 3 ouvertures. Par exemple :

label(1,apple).  label(2,banana).
label(3,carrot).  label(4,date).
label(5,eggfruit).
contains(1,apple). contains(2,eggfruit).
contains(3,date). contains(4,banana).
contains(5,carrot).

Cette variabilité vient du fait que, lorsqu'on ouvre la seconde boite, il y a deux possibilités concernant l'objet qu'elle contient, qui aurait dû se trouver dans une boite :

• que l'on a déjà trouvée comme mal étiquettée
• ou que l'on a pas encore pu décider

Par exemple, dans l'exemple précédent, si on ouvre la boite 4, on trouve que la boite 2 est mal étiquettée (car sensée contenir une banane). Si on ouvre la boite 5, on trouve la carotte, indiquant que la boite 3 est mal étiquettée. Les boites 2, 3, 4 et 5 étant invalidées, la bonne est bien la numéro 5. Maintenant, si plutôt que la 5 on avait ouvert la 3, on serait tombé sur la datte, qui ne nous aurait rien appris de plus que la 3 était mal étiquettée, puisque la boite 4, sensée contenir la datte, à déjà été ouverte.

On comprend donc pourquoi le puzzle, sur le site, utilise 4 boites, et pas plus : car à partir de 5 boites, il y a plusieurs réponses à la question.

Histoire de pouvoir explorer l'espace des solutions, comptons le nombre d'étape, et projetons le modèle sur le nombre de step :

#project nb_step/1.
#show nb_step/1.
nb_step(M):- M=#max{N:step(N)}.

Si vous ne connaissez pas project, qui sera présenté dans une annexe, dites vous que dans ce cas, lorsqu'il trouve plusieurs modèles avec les mêmes atomes nb_step/1, il n'en garde qu'un seul. Comme nous n'avons qu'un seul nb_step/1, qui donne le nombre d'ouvertures de boites, il aggrège les solutions en fonction de leurs tailles. Pratique.

Avec ce code à la place des #show déjà en place, et en appelant clingo avec l'option --project, on obtient :

clingo version 5.2.2
Reading from l.lp
Solving...
Answer: 1
nb_step(2)
Answer: 2
nb_step(3)
SATISFIABLE

Models       : 2
Calls        : 1
Time         : 0.013s (Solving: 0.00s 1st Model: 0.00s Unsat: 0.00s)
CPU Time     : 0.012s

Ok ! C'est tout bon, on a bien 2 ou 3 boites à ouvrir (selon la chance que l'on a). Si on relance clingo, mais cette fois-ci avec les 8 boites, on obtient des solutions de taille 4, 5 ou 6. En fait, plus on rajoute d'objets, plus il faut ouvrir de boites. Mais, selon la chance qu'on a, on peut avoir à en ouvrir seulement la moitié, ou les trois quarts.

exploration exhaustive

Enfin, bien que ce soit inutile, rien ne nous empêche de formuler le code pour qu'il cherche la réponse parmi toutes les combinaisons boite/objet possible. Pour cela, il faut bien évidemment retirer les déclarations explicites d'atomes contains/2, et il faut associer un objet à une boite et inversement :

% 1:1 association of boxes and items.
1 { contains(B,I): box(B)  } 1:- item(I).
1 { contains(B,I): item(I) } 1:- box(B).

Attention cependant : si on ne dit rien de plus, on aura droit à toutes les combinaisons possibles, par exemple des combinaisons où deux boites sont bien étiquettées, ou plus ! Avec une contrainte, on peut retirer les modèles qui décrivent une situation non voulue :

correct(B):- label(B,I) ; contains(B,I).
:- 1!={ correct(B): box(B) }.

Bon, maintenant, si on lance le code, c'est le gros dawa : il y a beaucoup plus de solutions possibles. Avec les 8 boites, on obtient 28560 solutions différentes.

Conclusions

Comme ASP ne nous permettais pas simplement de résoudre l'énigme, nous avons imaginé et implémenté l'algorithme qui nous permet de le faire. Et ainsi, avec une approche itérative, nous avons pu trouver la réponse à la question, et les réponses à des questions plus générales.

Notons aussi que, qui dit itératif, dit iterative solving, qui existe justement pour résoudre des problèmes de manière iterative, et que nous verrons dans une annexe dédiée en cours d'écriture.

L'approche temporelle est également possible ; cependant, c'est comme utiliser un bulldozer pour exploser une mouche, c'est-à-dire faire exactement ce qui a été fait dans cette quête annexe : utiliser le temps pour simuler l'itération.

Énigmes simples, deuxième fournée

Les énigmes suivantes viennent d'internet. Lorsqu'elles sont utilisées (en général sur les sites aggrégant ce genre d'énigme), aucun auteur n'est crédité.

Le coût de la vie

On sait qu'un bonnet et un ballon coûtent ensemble 1.10€, et que le bonnet coûte 1€ de plus que le ballon.

De par sa simplicité, cette énigme existe en beaucoup de variations, ne serais-ce que pour le nom des deux objets, mais aussi en utilisant des âges de personnes plutôt que des coûts.

Résolution en ASP

On peut simplement encoder le problème en donnant un choix sur le prix, et en indiquant des contraintes sur le choix. ASP va alors nous énumérer toutes les combinaisons possibles.

1{bonnet(1..110)}1.  % on choisi un coût pour chaque objet
1{ballon(1..110)}1.  %  (on compte en centime)

% le bonnet coûte 100 (1€) de plus que le ballon
bonnet(C+100):- ballon(C).

% Calculons le total
total(O+T):- bonnet(O) ; ballon(T).

% Assurons-nous qu'il atteint exactement 110 (1.10€)
:- total(N) ; N!=110.

Et le résultat est unique : il n'existe donc qu'une seule combinaison de prix qui corresponde à l'énoncé. Je vous laisse lancer clingo ou votre cerveau pour obtenir la réponse.

La Maison des Mères

Dans une famille, on trouve 2 mères, 2 filles, 1 grand-mère, et 1 petit-fille. Combien cette famille contient-elle de personnes ?

L'encoding de cette énigme est un poil long, mais, et c'est assez drôle, la majorité des règles sont finalement là pour expliquer les bases à l'ordinateur.

Le code source complet de la solution est là.

% Vu le phrasé de l'énigme, on considère que le nombre de mère
%  est égal au nombre de fille. Idem pour les grand-mères et petite filles.
% Donc on se contente de donner le nombre de (grand-)mère.
#const nb_mother=2.
#const nb_grandmother=1.

% Choix d'un nombre d'individus consécutifs
%  (comme 1,2,3, ou 1,2,3,4, mais pas 1,3,4 par exemple).
% C'est ça qui nous intéresse, pour répondre à la question.
indiv(1).
0 {indiv(N+1)} 1:- indiv(N) ; N<10.
:- indiv(I) ; not relation(I,_) ; not relation(_,I).  % an individual must be used

% Maintenant, on doit définir des liens familiaux,
%  et écarter ceux qui ne sont pas valides.

% On définit un ensemble de relation mère/fille.
%  on force un ordre arbitraire sur les individus pour éviter d'avoir
%  trop de solutions avec juste un ordre différents de nœud.
{mother(X,Y): indiv(X), indiv(Y), X<Y }.

% On déduit les autres relations à partir des relations mère/fille.
daughter(Y,X) :- mother(X,Y).
grandmother(X,Z) :- mother(X,Y) ; mother(Y,Z).
granddaughter(Z,X) :- mother(X,Y) ; mother(Y,Z).

% La notion de relation est une abstraction.
relation(X,Y):- mother(X,Y).
relation(X,Y):- grandmother(X,Y).
relation(X,Y):- daughter(X,Y).
relation(X,Y):- granddaughter(X,Y).

% Contrainte biologique à expliquer à l'ordinateur :
%  on n'a qu'une seule mère.
:- indiv(I) ; 2{mother(_,I)}.

% Écarte les modèles où on n'a pas le bon nombre de chaque relation.
:- not nb_grandmother{granddaughter(_,_)}nb_grandmother.
:- not nb_grandmother{grandmother(_,_)}nb_grandmother.
:- not nb_mother{mother(_,_)}nb_mother.
:- not nb_mother{daughter(_,_)}nb_mother.

Le sens de la famille

Notons que la question demande seulement le nombre de membres dans la famille. On peut donc, pour limiter aux réponses voulues, projetter sur indiv/1 et n'afficher que leur nombre :

% on compte et affiche uniquement le nombre d'individus.
nb_indiv(N):- N={indiv(_)}.
#show nb_indiv/1.
% si plusieurs modèles ont les mêmes atomes nb_indiv/1, on en garde un seul.
%  (nécessite l'option --project lors de l'appel à clingo)
#project nb_indiv/1.

Mais voilà : c'est un peu nul, car on ne fait que répondre à la question, sans comprendre pourquoi on arrive à ce nombre exact de personnes dans la famille. Et si on affichait l'arbre généalogique, plutôt ?

Voire avec ses yeux

Histoire de visualiser les solutions, plutôt que projeter le nombre d'individu et n'afficher que le résultat, on peut utiliser biseau :

link(X,Y):- mother(X,Y).
label(X,Y,mother):- mother(X,Y).
obj_property(edge,arrowhead,normal).

Et, avec la commande python -m biseau encoding.lp -o "out-{}.png", qui créé un graphe pour chaque solution, on obtient l'unique arbre généalogique suivant :

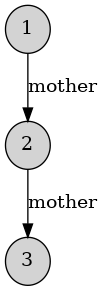
Lorsque l'on changera le nombre attendu de mères et grand-mères (essayez 4 mères et 2 grands-mères par exemple, c'est le cas typique), on verra que beaucoup d'autres solutions sont proposées, mais aussi que la majorité sont des répétitions inutiles : seul le nom des nœuds changent.

Aussi, un autre type de famille apparaîtra, et en très grand nombre : celles qui se composent en réalité de deux arbres généalogiques indépendant. Zut, c'est pas ce qu'on voulait.

Liens du sang

La contrainte manquante : que tout le monde soit de la même famille, autrement dit, que tous les membres de la famille soient liés. Du code sera nécessaire pour s'assurer qu'aucune composante connexe ne se trouve dans le graphe final :

% On doit tous appartenir à la même famille.
path(X,Y):- relation(X,Y).
path(X,Z):- relation(X,Y) ; path(Y,Z).
:- indiv(I) ; indiv(J) ; I<J ; not path(I,J).

Bim bam boum, voilà ! Avec 4 mères et 2 grand-mères, on passe de 51 solutions à 11. Pas mal ! Mais c'est encore insuffisant : de nombreuse symmétries permettent à deux solutions de notre point de vue identique d'exister indépendamment l'une de l'autre.

Suppression d'autres symmétries

Pour supprimer toutes les symmétries inutiles pour le cas avec 4 mères et 2 grand-mères, voici trois contraintes. Si vous les ajoutez et générez les images, vous ne trouverez que les trois solutions possibles, sans les répétitions :

% Une nièce doit être plus grande que sa tante.
:- indiv(I) ; indiv(J) ; I<J ; mother(M,J), grandmother(M,I).
% Une sœur plus petite ne peut avoir d'enfant si les plus grandes n'en ont pas.
:- indiv(I) ; indiv(J) ; I<J ; mother(M,I) ; mother(M,J) ; mother(I,_) ; not mother(J,_).
% La sœur la plus grande a l'enfant le plus grand.
:- indiv(I) ; indiv(J) ; I<J ; mother(M,I) ; mother(M,J) ; mother(I,X) ; mother(J,Y) ; X>Y.

(Évidemment, ici, par «la plus grande», on sous-entends bien que c'est le numéro d'individu qui est plus grand, rien à voir avec la taille, le poids ou que-sais-je, qui n'ont aucun intérêt dans la question)

Enlevez n'importe laquelle de ces trois contraintes, et vous aurez des doublons. Avec ces trois contraintes complètement arbitraires, on obtient bien seulement 3 cas bien différents en topologie.

Si vous vous demandez pourquoi, retirez une contrainte, et regardez les doublons qui apparaissent. Ces trois contraintes ne sont en fait que l'énonciation «humanisée» de trois contraintes :

• un nœud avec N prédécesseurs a un identifiant plus grand que celui d'un nœud avec moins de N successeurs
• pour deux nœuds ayant le même prédécesseur, celui ayant l'identifiant le plus petit ne peux avoir de successeur si l'autre n'en a pas
• le nœud ayant le plus grand identifiant parmi les successeurs d'un nœud N sera aussi le prédecesseur du nœud de plus grand identifiant parmis tous les successeurs des successeurs de N.

Ces contraintes, je les ai imaginées en regardant les doublons. En testouillant un peu, j'ai vu qu'elles fonctionnaient encore bien avec d'autres valeurs (6 mères, 3 grand-mères), mais laissaient passer quelques doublons. Peut-être est-il possible de trouver des contraintes qui suppriment les doublons dans tous les cas ? L'autre solution serais de comparer a posteriori tous les graphes entre eux, en ne regardant que la topologie. Mais c'est un problème complexe.

Énigme d'Einstein

Vous vous en souvenez certainement : cette énigme occupe les repas de famille tous les ans, sans qu'aucune solution ne soit trouvée. Elle est très bien expliquée ici, ainsi que deux méthodes de résolutions possibles : avec la tête, ou algorithmiquement.

En gros, selon certains indices, il faut savoir qui parmis l'anglais, le norvégien, le suédois, le danois et l'allemand possède les poissons. La modélisation du problème est un poil longue, car il y a beaucoup de relations à écrire, et aussi beaucoup d'évidences.

Le code source complet est là. Allons-y ensembles, pas-à-pas…

Les données

humain(anglais;suedois;danois;norvegien;allemand).
couleur(rouge;bleue;jaune;verte;blanche).
animal(chiens;oiseaux;cheval;chats;poisson).
boisson(lait;biere;the;cafe;eau).
fume(dunhill;blue_master;blend;prince;pall_mall).

% Les maisons sont proches selon leur place.
next(1,2). next(2,3). next(3,4). next(4,5).
next(X,Y) :- next(Y,X).  % réciprocité

Les évidences

% Chaque humain a une couleur de maison.
1 { maison(H,C): couleur(C) } 1 :- humain(H).
% Chaque couleur de maison a un humain.
1 { maison(H,C): humain(H) } 1 :- couleur(C).

% Chaque humain a un animal.
1 { animal(H,A): animal(A) } 1 :- humain(H).
% Chaque animal a un humain.
1 { animal(H,A): humain(H) } 1 :- animal(A).

% Pareil pour la boisson…
1 { boisson(H,B): boisson(B) } 1 :- humain(H).
1 { boisson(H,B): humain(H) } 1 :- boisson(B).

% Pareil pour le tabac…
1 { fume(H,F): fume(F) } 1 :- humain(H).
1 { fume(H,F): humain(H) } 1 :- fume(F).

% Pareil pour la place de maison…
1 { place_maison(H,P): next(P,_) } 1 :- humain(H).
1 { place_maison(H,P): humain(H) } 1 :- next(P,_).

Rien de très intéressant ici. Notez que, pour faire une association 1-pour-1 parfait, deux règles sont nécessaires : l'une pour dire qu'il y a un humain pour chaque chose, et une autre pour dire qu'il y a une chose pour chaque humain. Retirez une seule de ces règles, et vous obtenez des solutions où des humains se partagent des objets ou inversement.

Généralisations des valeurs

Notez qu'en plaçant le nom des objets (boisson, fume, couleur, animal, place) comme argument d'un atome, on pourrait n'avoir besoin d'écrire qu'une seule fois ces règles d'assignation:

humain(anglais;suedois;danois;norvegien;allemand).
objet(fume,(dunhill;blue_master;blend;prince;pall_mall)).
objet(couleur,(rouge;bleue;jaune;verte;blanche)).
objet(animal,(chiens;oiseaux;cheval;chats;poisson)).
objet(boisson,(lait;biere;the;cafe;eau)).

objet(O) :- objet(O,_).

1 { association(H,O,V): objet(O,V) } 1 :- humain(H) ; objet(O).
1 { association(H,O,V): humain(H) } 1 :- objet(O,V).

Voilà une piste d'amélioration — que nous n'utiliserons pas ici — permettant de gérer des instances du problème avec un nombre arbitraire d'objets.

Les indices

% 1. L'Anglais vit dans une maison rouge.
maison(anglais,rouge).

% 2. Le Suédois a des chiens comme animaux domestiques.
animal(suedois,chiens).

% 3. Le Danois boit du thé.
boisson(danois,the).

% 4. La maison verte est juste à gauche de la maison blanche.
:- maison(H1,blanche) ; place_maison(H1,Pb) ; maison(H2,verte) ; place_maison(H2,Pv) ; Pb-Pv!=1.

% 5. Le propriétaire de la maison verte boit du café.
boisson(P,cafe) :- maison(P,verte).

% 6. La personne qui fume des Pall Mall a des oiseaux.
fume(P,pall_mall) :- animal(P,oiseaux).

% 7. Le propriétaire de la maison jaune fume des Dunhill.
maison(P,jaune) :- fume(P,dunhill).

% 8. La personne qui vit dans la maison du centre boit du lait.
place_maison(P,3) :- boisson(P,lait).

% 9. Le Norvégien habite la première maison.
place_maison(norvegien,1).

% 10. L'homme qui fume les Blend vit à côté de celui qui a des chats.
fume(P,blend) :- place_maison(P,MaisonP) ; next(MaisonP,MaisonChat) ; place_maison(HommeChat,MaisonChat) ; animal(HommeChat,chats).

% 11. L'homme qui a un cheval est le voisin de celui qui fume des Dunhill.
animal(P,cheval) :- place_maison(P,MaisonP) ; next(MaisonP,MaisonDunhill) ; place_maison(HommeDunhill,MaisonDunhill) ; fume(HommeDunhill,dunhill).

% 12. Le propriétaire qui fume des Blue Master boit de la bière.
boisson(P,biere) :- fume(P,blue_master).

% 13. L'Allemand fume des Prince.
fume(allemand,prince).

% 14. Le Norvégien vit juste à côté de la maison bleue.
maison(Autre,bleue) :- next(PlaceNorvegien,PlaceAutre) ; place_maison(Autre,PlaceAutre) ; place_maison(norvegien,PlaceNorvegien).

% 15. L'homme qui fume des Blend a un voisin qui boit de l'eau
fume(P,blend) :- place_maison(P,MaisonP) ; next(MaisonP,MaisonEau) ; place_maison(HommeEau,MaisonEau) ; boisson(HommeEau,eau).

L'horreur de l'indice 14

L'indice 14 est piégeant. Une première manière de l'écrire pourrait être le suivant :

place_maison(norvegien,PlaceNorvegien) :- next(PlaceNorvegien,PlaceAutre) ; place_maison(Autre,PlaceAutre) ; maison(Autre,bleue).

Mais attention ! Cette règle rendra le problème insoluble. Cela peut paraître un tantinet capillotracté, mais il est important de le comprendre : il y a deux atomes next(PlaceNorvegien,PlaceAutre) valides pour une maison bleue donnée (la maison à sa gauche, et la maison à sa droite). Or, avec cette écriture, on indique au solveur que pour chaque maison à côté, on a place_maison(norvegien,PlaceNorvegien). Et c'est là qu'est l'os : le norvegien ne peut être à deux endroits en même temps.

Mais alors, me diriez-vous, pourquoi dans le code plus haut, cette écriture est-elle valide ?

maison(Autre,bleue) :- next(PlaceNorvegien,PlaceAutre) ; place_maison(Autre,PlaceAutre) ; place_maison(norvegien,PlaceNorvegien).

On reconnaît le problème dû au next/2 rencontré dans la formulation au dessus. Mais là, a priori sans raison, cette expression fonctionne. Et cela est dû à un cas particulier : la place de la maison du norvégien est fixée à 1, à cause de l'indice 9. Par conséquent, next(PlaceNorvegien,PlaceAutre) est traduit next(1,PlaceAutre) par le grounder, qui n'est vrai qu'avec un seul atome : next(1,2).

C'est donc un cas particulier qui nous permet d'écrire la règle ainsi. En réalité, il faudrait dire qu'exactement un voisin du norvégien vit dans une maison bleue :

1 { maison(Autre,bleue): next(PlaceNorvegien,PlaceAutre), place_maison(Autre,PlaceAutre) } 1 :- place_maison(norvegien,PlaceNorvegien).

Et là, effectivement, ça fonctionne. Notez qu'avec cette écriture, vous pouvez supprimer l'indice 9, et vous obtiendrez deux modèles qui répondent de manière identique pour le propriétaire des poissons. Enfin, si vous regardez bien les autres indices, vous verrez que les indices 10, 11 et 15 sont de la même facture. Et, comme pour le 14, une subtilité dans les indices permet d'éviter une limitation explicite du nombre de voisins. C'est pas hyper robuste, mais c'est plus rapide pour le solveur.

Réponse… (SPOILER)

Et la réponse est… L'allemand. En effet, le seul answer-set donné par le solveur indique bien, entre autre, l'atome animal(allemand,poisson). Évidemment, toutes les assocations sont données, par exemple fume(danois,blend), qui ne peut être deviné lorsque l'on déroule l'énigme que dans les dernières étapes.

Trop facile !

Clairement, cette énigme d'einstein est trop simple : certains indices sont juste là pour aider les humains !

la prochaine fois que vous la poserez, ne donnez pas les indices 1 et 9. Essayez : clingo vous donne plusieurs solutions possible, mais le possesseur des poissons reste le même.

Eh ! Et si on faisait un code Python qui cherchait à minimiser le nombre de règles à donner ? Allez ! Le voici :

import os
import itertools
import clyngor


ASP_SRC_BASE = """
% Les données
humain(anglais;suedois;danois;norvegien;allemand).
couleur(rouge;bleue;jaune;verte;blanche).
animal(chiens;oiseaux;cheval;chats;poisson).
boisson(lait;biere;the;cafe;eau).
fume(dunhill;blue_master;blend;prince;pall_mall).

% Les maisons sont proches selon leur place.
next(1,2). next(2,3). next(3,4). next(4,5).
next(X,Y) :- next(Y,X).  % réciprocité

% Chaque humain a une couleur de maison.
1 { maison(H,C): couleur(C) } 1 :- humain(H).
% Chaque couleur de maison a un humain.
1 { maison(H,C): humain(H) } 1 :- couleur(C).

% Chaque humain a un animal.
1 { animal(H,A): animal(A) } 1 :- humain(H).
% Chaque animal a un humain.
1 { animal(H,A): humain(H) } 1 :- animal(A).

% Pareil pour la boisson…
1 { boisson(H,B): boisson(B) } 1 :- humain(H).
1 { boisson(H,B): humain(H) } 1 :- boisson(B).

% Pareil pour le tabac…
1 { fume(H,F): fume(F) } 1 :- humain(H).
1 { fume(H,F): humain(H) } 1 :- fume(F).

% Pareil pour la place de maison…
1 { place_maison(H,P): next(P,_) } 1 :- humain(H).
1 { place_maison(H,P): humain(H) } 1 :- next(P,_).
"""

ASP_RULES = (  # set of rules narrowing the solutions
    'maison(anglais,rouge).',
    'animal(suedois,chiens).',
    'boisson(danois,the).',
    ':- maison(H1,blanche) ; place_maison(H1,Pb) ; maison(H2,verte) ; place_maison(H2,Pv) ; Pb-Pv!=1.',
    'boisson(P,cafe) :- maison(P,verte).',
    'fume(P,pall_mall) :- animal(P,oiseaux).',
    'maison(P,jaune) :- fume(P,dunhill).',
    'place_maison(P,3) :- boisson(P,lait).',
    'place_maison(norvegien,1).',
    'fume(P,blend) :- place_maison(P,MaisonP) ; next(MaisonP,MaisonChat) ; place_maison(HommeChat,MaisonChat) ; animal(HommeChat,chats).',
    'animal(P,cheval) :- place_maison(P,MaisonP) ; next(MaisonP,MaisonDunhill) ; place_maison(HommeDunhill,MaisonDunhill) ; fume(HommeDunhill,dunhill).',
    'boisson(P,biere) :- fume(P,blue_master).',
    'fume(allemand,prince).',
    '1 { maison(Autre,bleue): next(PlaceNorvegien,PlaceAutre), place_maison(Autre,PlaceAutre) } 1 :- place_maison(norvegien,PlaceNorvegien).',
    'fume(P,blend) :- place_maison(P,MaisonP) ; next(MaisonP,MaisonEau) ; place_maison(HommeEau,MaisonEau) ; boisson(HommeEau,eau).',
)


def rules_are_valid(rules_indexes:{int}) -> bool:
    "True if the set of rules yield only good solutions"
    rules_indexes = set(rules_indexes)
    asp = ASP_SRC_BASE + ''.join(rule for idx, rule in enumerate(ASP_RULES, start=1) if idx in rules_indexes)
    for model in clyngor.solve(inline=asp).by_predicate:
        for *human, animal in model['animal']:
            # NB: human may be a list containing a nationality (allemand, suedois,…)
            #  or an empty list. Beware !
            if human == ['allemand'] and animal != 'poisson':
                return False
            elif human and human != ['allemand'] and animal == 'poisson':
                return False
    return True


def powerset(iterable, minsize=0):
    "powerset([1,2,3]) --> () (1,) (2,) (3,) (1,2) (1,3) (2,3) (1,2,3)"
    s = list(iterable)
    return itertools.chain.from_iterable(itertools.combinations(s, r) for r in range(minsize, len(s)+1))

def compute_valid_sets_of_rules(minsize:int=10) -> [frozenset]:
    "Yield the valid sets of rules"
    for rules in powerset(range(1, 16), minsize=minsize):
        rules = tuple(rules)
        if rules_are_valid(rules):
            yield frozenset(rules)

def filter_suboptimal_valid_sets(valid_sets:[frozenset]) -> [frozenset]:
    """Yield given valid sets, except those that are superset of others.

    Example: the valid set {a, b, c} is not yielded if {a, b} is also a valid set

    """
    for valid_set in valid_sets:
        if not any(other_valid_set < valid_set for other_valid_set in valid_sets):
            yield valid_set

def write_valid_sets(valid_sets, minsize:int=10):
    "Write valid sets in the dedicated module"
    valid_sets = tuple(valid_sets)
    with open('meteinstein_data.py', 'w') as fd:
        fd.write(f'# File generated by meteinstein_riddle.py\n\n')
        fd.write(f'# valid sets of rules with at least {minsize} elements\n')
        fd.write('valid_sets = {  # exclude suboptimal ones\n')
        for valid_set in filter_suboptimal_valid_sets(valid_sets):
            fd.write('\tfrozenset((' + ', '.join(map(str, sorted(tuple(valid_set)))) + ')),\n')
        fd.write('}\n\n')
        fd.write('all_valid_sets = {  # including the suboptimals\n')
        for valid_set in valid_sets:
            fd.write('\tfrozenset((' + ', '.join(map(str, sorted(tuple(valid_set)))) + ')),\n')
        fd.write('}\n')


def rules_statistics(valid_sets) -> [(str, str)]:
    "Yield pairs (metric, value)"
    necessary_rules = frozenset.intersection(*valid_sets)
    yield 'necessary rules', ', '.join(map(str, necessary_rules))
    yield 'minimal rule number', min(map(len, valid_sets))
    yield 'useless rules', ', '.join(map(str, (set(range(1, 16)) - frozenset.union(*valid_sets)) or ['none']))

def rule_context_asp_repr(valid_sets) -> [str]:
    "Yield lines representing context in ASP format, as rel/2 atoms"
    for idx, rules in enumerate(sorted(tuple(valid_sets)), start=1):
        for rule in rules:
            yield f'rel(ans{idx},r{rule}).'

if __name__ == '__main__':
    if not os.path.exists('meteinstein_data.py'):
        write_valid_sets(compute_valid_sets_of_rules())

    from meteinstein_data import valid_sets

    for metric, value in rules_statistics(valid_sets):
        print(metric + ':', value)

    with open('meteinstein-riddle.lp', 'w') as fd:
        for line in rule_context_asp_repr(valid_sets):
            fd.write(line + '\n')

Ok, c'est carrément bourrin, mais le principe est bon : on teste toutes les combinaisons de règles avec au moins 9 d'entre elles. Et qu'apprend-t-on ?

Que les règles 2, 3, 6, 10, 11, 12 et 13 sont nécessaires : virez-en une seule, et l'énoncé permet à plusieurs humains d'avoir les poissons. Autrement dit, sans elles, le problème est mal posé. Cependant, ces 7 règles ne sont pas suffisantes: en effet, il faut au moins trois autres règles — les 8, 9 et 15 — pour avoir un énoncé propre qui ne laisse qu'un seul propriétaire possible aux poissons.

On constate qu'il existe au total 48 énoncés différents possibles qui mènent à la solution, dont 8 sont réellement différents les uns des autres (intuitivement, si une solution ayant 10 règles est valide, alors une solution avec les mêmes 10 règles et 1, 2, 3 ou 4 autres en plus est aussi valide, c'est pourquoi on arrive à 48 énoncés).

Les 8 solutions peuvent être montrées de plein de manières différentes : un treillis de Galois, par exemple !

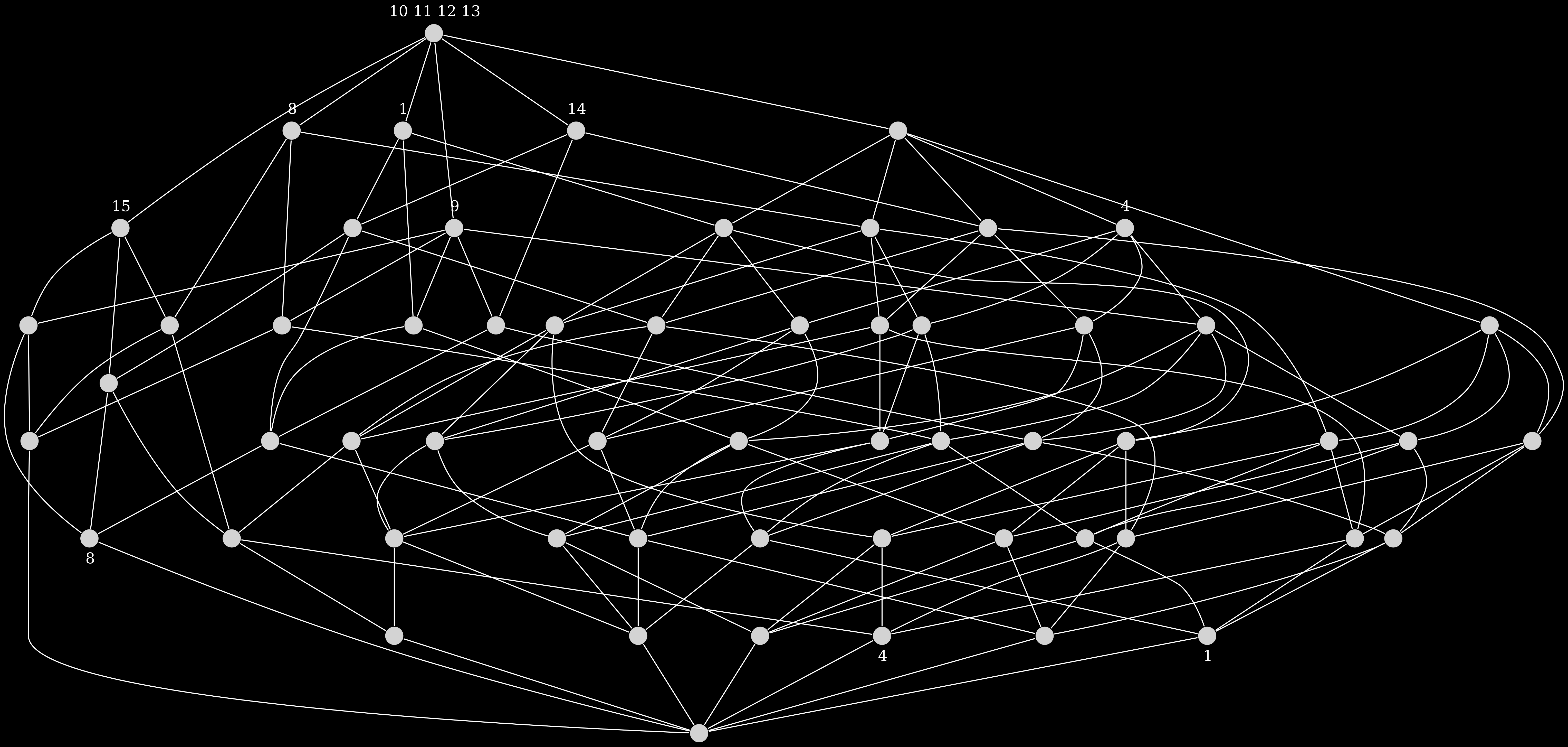
Le treillis n'est pas très aidant, car trop gros… Regardons la compression alors !

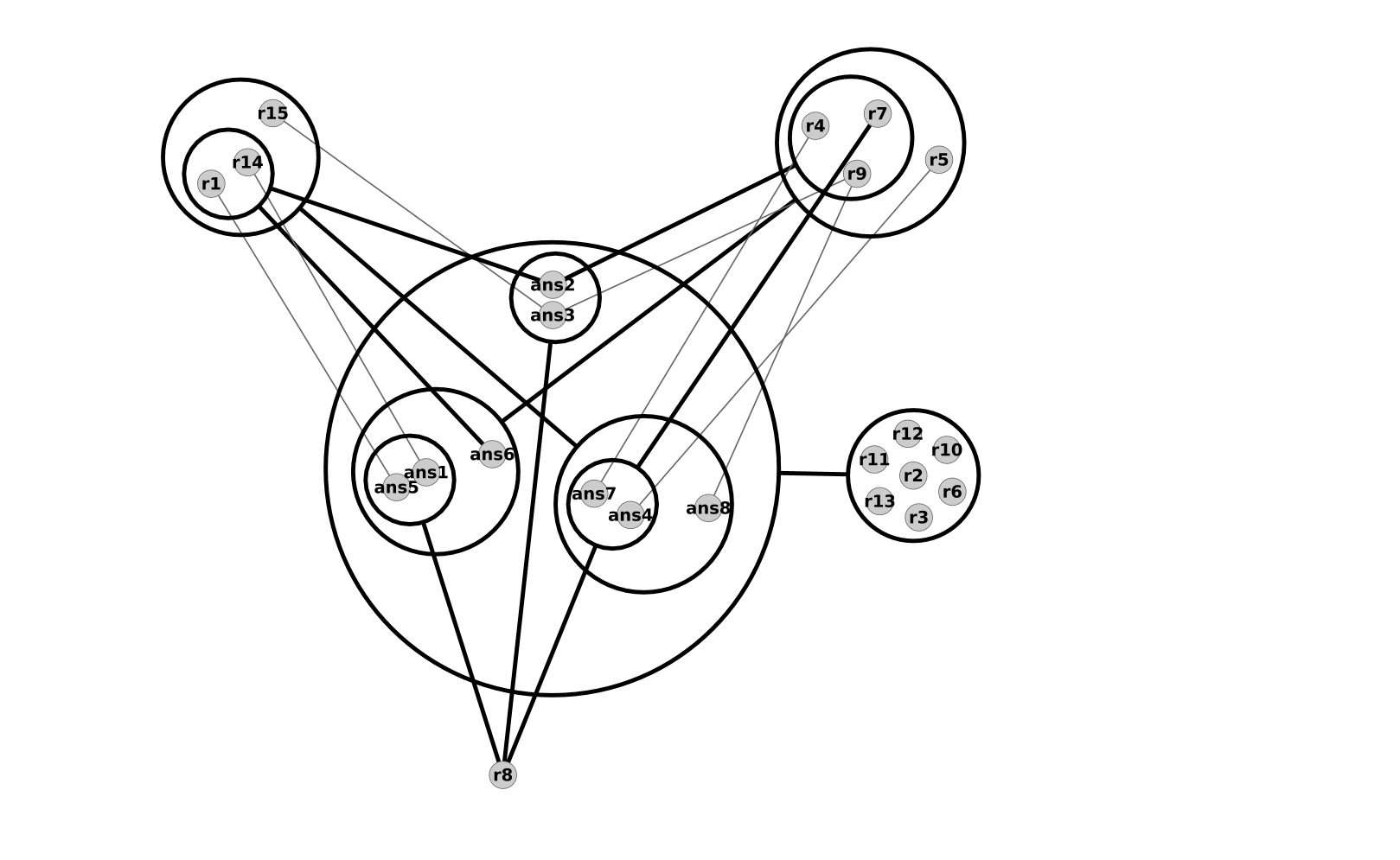
Bof. On voit bien les règles nécessaires, regroupées à droite, mais les autres relations sont pas des masses claires…

Bon, ben, un bête tableau…

              Règles à ajouter
           1  4  5  7  8  9 14 15
réponse 1:             X  X     X       -> la meilleure !
réponse 2:    X  X  X  X  X  X
réponse 3: X              X  X  X
réponse 4: X     X  X  X     X  X
réponse 5: X  X     X  X     X  X
réponse 6: X  X     X  X  X  X
réponse 7: X  X  X  X     X  X
réponse 8: X  X  X  X  X  X

On note qu'il y a toujours au moins deux trous : il y a autrement dit toujours au moins deux règles en trop :)

On note aussi que le tableau est très rempli… et si on créait un treillis et un graphe, mais sur le tableau inversé ?

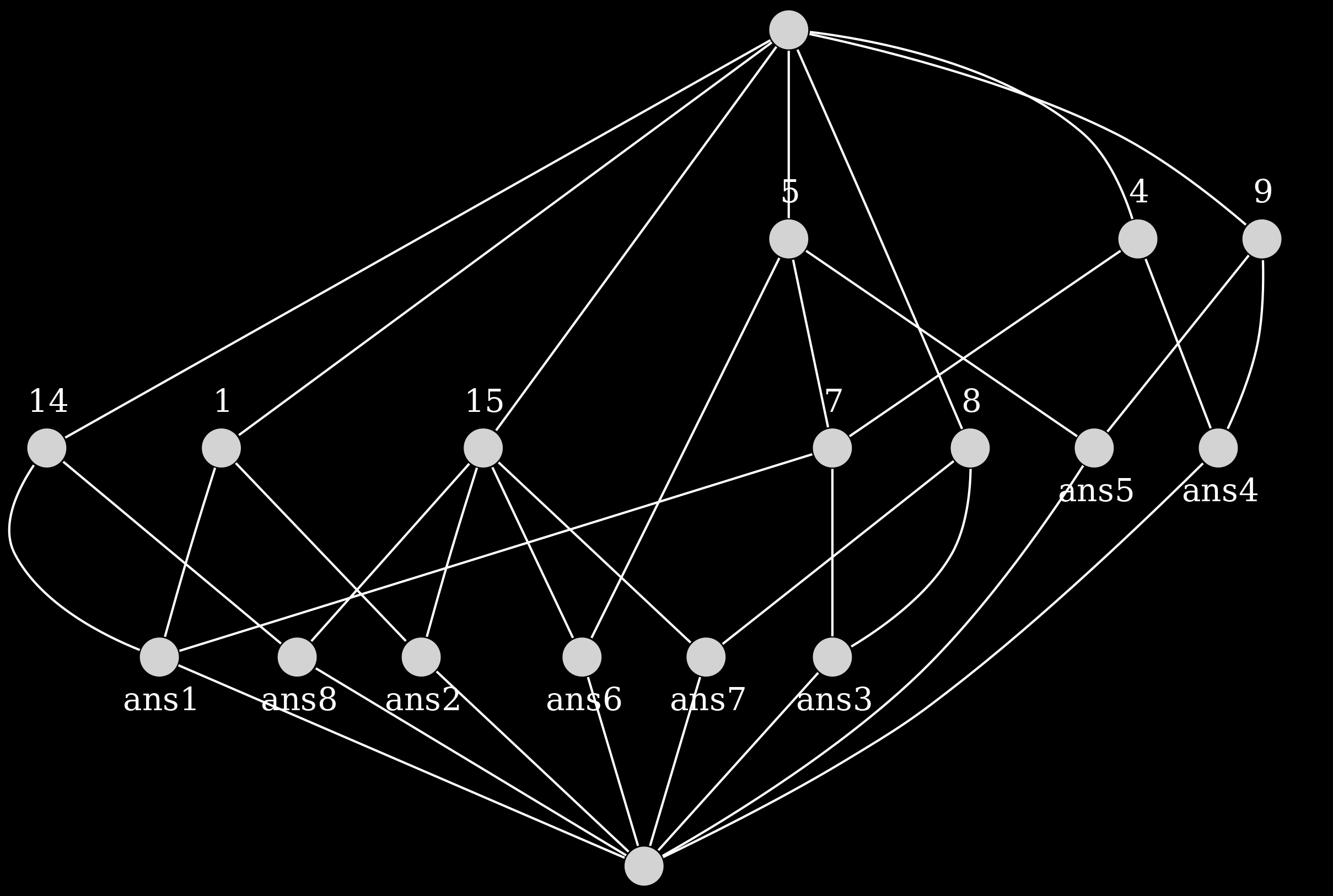
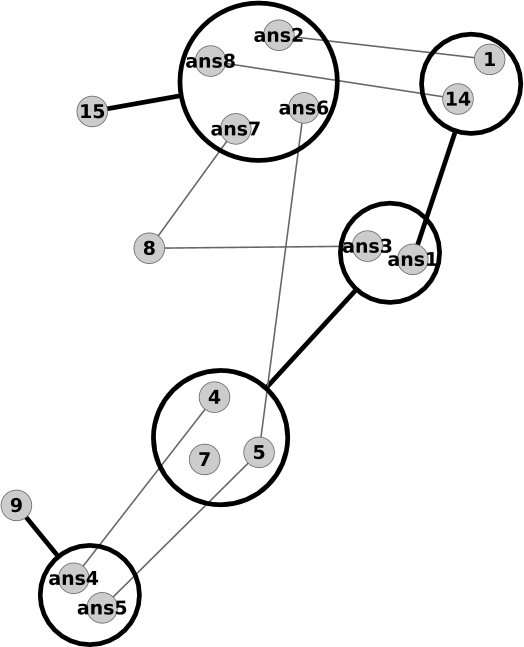
Bim ! Et voilà des structures plus compréhensibles ! On peut y lire par exemple :

• le nœud affublé de ans1 signifie que la réponse 1 est dans ce concept et tous ceux qui lui sont supérieurs
• le nœud affublé de 14 signifie que la règle 14 n'est pas utilisée par les réponses dans ce concept et ceux qui lui sont inférieurs
• la règle 8 n'est pas utilisée par les réponse 3 et 7
• on voit très bien la règle numéro 15 juste au-dessus des 4 réponses où elle n'apparaît pas

Au final, ça reste décevant, car c'est vachement intriqué. On remarque cependant la place particulière des règles 4, 5 et 15, qui sont présentes dans beaucoup de concepts, montrant une certaine absence dans les données ; en d'autres termes, ce sont clairement les règles les plus dispensables de l'énigme.

Bref, conclusion de tout ça : Einstein était vraiment gentil.

Conclusion

Pour certains jeux de logique, ASP est utile. Même quand les relations s'accumulent, ou que l'instance grossie, il reste possible d'obtenir un code relativement simple qui réponde à la question.

Quelles énigmes ASP ne peut-il pas résoudre directement ? Eh bien, beaucoup. Notamment ceux qui font appelle à la logique épistémologique, ou demandent l'élaboration de protocoles. Ou alors, comme on l'a vu dans la partie dédiée, il faut élaborer une recherche de la solution sois-même, il ne suffit plus de décrire le problème. Heureusement, de nombreuses techniques permettent de se simplifier la vie, même dans ces cas complexes, par exemple les variantes du solving (que nous verrons dans une (quête) annexe dédiée),

ou la logique temporelle.