Cet article est une quête annexe du tuto général pour ASP, s'intéressant aux bases de l'écriture de propagateurs en python, ces objets qui permettent de suivre l'évolution du solving en temps réel, pour le regarder, l'aider, et même le modifier.
Je considère dans la suite Python comme un langage acquis. Au besoin, allez faire un tour du côté de Swinnen. S'il vous manque les notions de POO (bien qu'on en utilise moins de 1% ici), allez voir sam et max.
On commence avec une présentation théorique, suivis de trois exemples rigolos (mais néanmoins utiles !) et d'un cas pratique consistant à écrire des contraintes ASP en Python.
Extending avec Python : Propagateurs
Vous avez déjà étendu Python avec du C pour gagner un peu en performances ? Eh bien, de la même manière, on peut mettre du Python (ou du Lua) dans ASP pour profiter, pendant le solving même, de la puissance d'un langage impératif. C'est ce qu'on nomme embedding ou extending, selon le point de vue. Ici, nous allons voir comment embarquer du Python dans ASP, ou, c'est équivalent, étendre ASP avec Python.
Les propagateurs sont des objets assez connus dans le monde du solving. Il s'agit plus ou moins d'un plugin qui va pouvoir suivre et modifier le déroulement de l'heuristique. Pour être encore plus précis : un propagateur permet d'écrire des contraintes en Python plutôt qu'en ASP.
Avec Python et un peu de connaissance sur clingo, il est possible d'écrire un propagateur pouvant, par exemple, changer la véracité de certains atomes en fonction de celle d'autres atomes.
Notez que l'API officielle de clingo est nécessaire ici. Si vous ne l'avez pas, vous ne pourrez pas exécuter les exemples (mais vous pourrez les comprendre quand même, notre cerveau ne s'embarassant pas de problèmes mondains tels que les dépendances).
Sous le capot de clingo
Clingo, en interne, ne s'amuse pas à manipuler les atomes via leurs symboles (comme p(5) ou q(a,b,c(p(a,b("e"),d)))),
sous la forme de chaîne de caractères ou d'objets plus complexes.
La raison est simple : c'est inefficace, d'autant que clingo se fiche de savoir que tel atome a tel predicat et tel arguments : il s'intéresse uniquement aux propagations qu'il peut faire selon les règles qu'on lui a fournis.
Par exemple, p(5):- p(4). devient pour clingo quelque chose comme 12 :- 45,
qui indique que l'atome 12 est vrai si l'atome 45 l'est. Une table en mémoire permettra
de retrouver la correspondance avec les symboles p(5) et p(4) lorsqu'il faudra les afficher à l'utilisateur.
Ici, j'ai choisi les entiers 12 et 45 au hasard, mais clingo, d'après ce que j'ai vu, les numérote à partir de 1, dans l'ordre où il les rencontre. C'est donc, de notre point de vue d'utilisateur extérieur, aléatoire. Notez que cette compilation des symboles aux identifiants uniques est permise par l'expension des variables au grounding, i.e. le fait que gringo va remplacer une règle contenant une variable par toutes les règles possibles ; le solveur ne manipule de fait aucune variable, juste des état de vérité pour des atomes.
Revenons à nos moutons : clingo manipule des entiers, qui sont appelés officiellement des solver literals, ou litéraux du solver.
Ces litéraux du solveur ne changent pas durant tout le solving, et ce sont les éléments de base qu'un propagateur va manipuler.
Le solveur associe à ces littéraux une des trois valeurs de vérité suivante : vrai, faux, non valide.
Au tout départ, tous les atomes sont non valides, sauf ceux dont vous indiquez la véracité par défaut, par exemple avec l'expression a. : l'atome a sera toujours vrai.
Puis, en respectant les règles comme p(X):- q(X) ; r(X)., le solveur va pas-à-pas changer les valeurs de vérité des atomes.
Si à un moment il s'aperçoit que ce qu'il fait est impossible (car une contrainte devient vraie par exemple),
il backtrack, c'est-à-dire qu'il va revenir en arrière, pour essayer d'autres combinaisons.
Et si à un moment tous les atomes ont une valeur de vérité vraie ou fausse, et qu'aucune contrainte n'est violée, alors le solveur sait qu'il s'agit d'un ensemble réponse : il affiche alors tous les atomes ayant une valeur de vérité vraie (en utilisant la table de correspondance numéro ⇔ symbole).
Un propagateur va pouvoir agir à différents moments : au début, lorsque le solveur découvre les atomes, lorsque le solveur propose une valeur de vérité pour un atome (on dit alors qu'il propage), lorsqu'il backtrack, ou lorsqu'il a dans les mains un answer-set valide.
Voici un exemple de code ASP :
a;b.
c;d:-a.
e;f:-b.
(Si vous ne comprenez pas bien ce qu'il fait, lancez clingo dessus. N'oubliez pas de regarder tous les answer-set)
Et voici comment clingo explore l'espace :
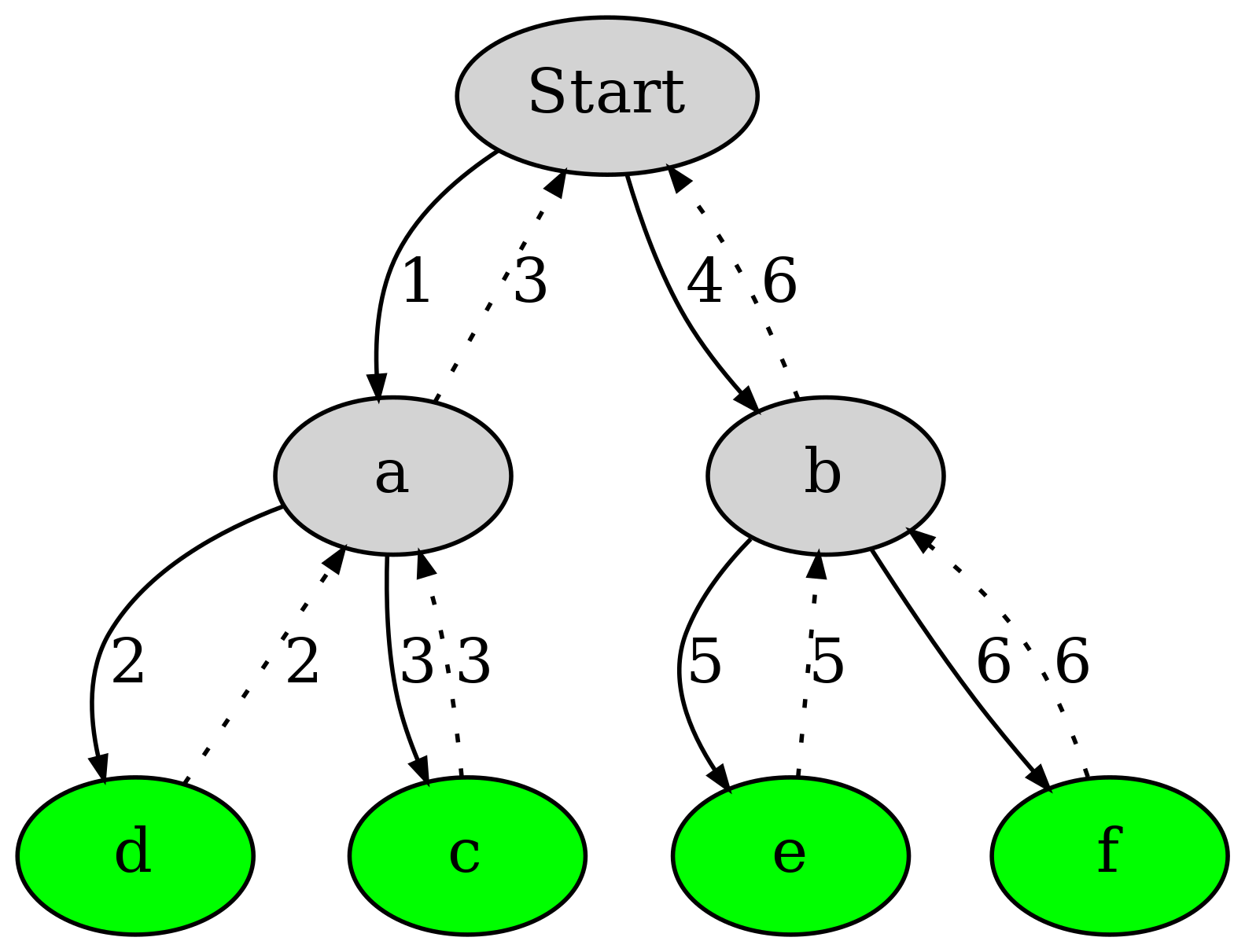
Pour lire le dessin : les ellipses sont des décisions du solving où l'atome indiqué est décidé vrai, reliés par une flèche pleine pour symboliser une assignation du solveur, des flèches en pointillé pour symboliser les backtracks, et les numéros indiquent dans quel ordre il faut suivre les flèches. Les nœuds verts correspondent à un modèle généré par le solveur.
Suivons l'aventure pas-à-pas. Au début, clingo considère que tous les atomes sont de valeur non déterminée, et dans le dessin cet état est indiqué par le nœud Start. Ensuite, en première étape (flèche 1) clingo va assigner vrai à b. Puis à l'étape 2, vrai à f. On devine qu'en même temps les atomes a et e sont mis à faux (car ils ne peuvent pas être vrais en même temps que b et f d'après le programme), ainsi que c et d, qui ne peuvent pas être vrais car a est faux (toujours d'après le programme).
Tous les atomes possèdent une valeur de vérité : il s'agit donc d'un modèle possible et c'est pourquoi le nœud f est vert. Lorsque clingo atteint cet état, il affiche à l'écran tous les symboles des atomes dont la valeur de vérité est vraie.
Ensuite, il backtrack : il revient sur le nœud b. C'est là qu'il choisi différemment qu'à l'étape 2, c'est-à-dire e comme vrai ; f est alors faux, et comme tous les atomes ont une valeur de vérité, il peut sortir le modèle (c'est pourquoi e est également en vert).
Et là, double backtrack : il revient sur b, constate qu'il a exploré tous les choix possible, donc revient encore jusqu'à start, où là un autre choix n'a pas encore été exploré : décider a comme vrai. Ce qui est fait à l'étape 4, et comme pour b, on assiste à une exploration de chaque possibilité avec un backtrack pour revenir sur a. Lorsque toutes les possibilités ont été épuisées, le solver backtrack encore, revenant sur Start. Sauf que maintenant… il n'y a plus rien à explorer. C'est donc la fin du solving, tous les modèles ont été générés.
Les 4 cavaliers
Un propagateur, en python, est une classe présentant au moins une de ces 4 méthodes :
init: appelée une seule fois, en première ; c'est là qu'on prend connaissance des littéraux du solveur choisis pour chaque atomepropagate: appelée chaque fois que l'heuristique va donner une valeur de vérité à un littéral (dire qu'un atome est vrai ou faux)undo: appelée chaque fois que l'heuristique va retirer une valeur de vérité à un littéralcheck: appelée chaque fois que l'heuristique vérifie le modèle qu'elle possède
(détail important : le init n'a rien à voir avec __init__, utilisée en python pour initialiser les objets)
Vérification de modèle et vérité des litéraux
Comme nous avons vu au début, un atome est soit vrai, soit faux.
Ceci est faux : un atome peut également être dans un état indéterminé. Si nous ne l'avons jamais vu, c'est parce que cet état n'est possible que lorsque l'heuristique cherche pour un modèle valide. Pendant cette recherche, l'heuristique va donner des valeurs de vérité (vrai ou faux) aux atomes, chacun à leur tour, explorant les différentes possibilités.
Lorsque tous les atomes ont une valeur de vérité (on parle alors d'assignement total, en opposition à un assignement partiel où ne sont assignés à une valeur de vérité qu'une partie des atomes), il faut décider si le modèle est valide, c'est-à-dire si les valeurs de vérité (l'assignation) n'entre en conflit avec aucune contrainte.
(en réalité, la vérification des contraintes se fait au fur et à mesure, sur les assignements partiels, histoire d'éviter de chercher un assignement total là où de toute façon on trouve une contradiction ; autrement dit, les contraintes élaguent l'espace de recherche)
C'est le dernier moment pour les contraintes pour montrer que l'assignement total entre en conflit avec une contrainte, prouvant que le modèle n'est pas valide, et donc qu'il n'a pas a être écrit en sortie de programme.
Et tout ce processus pourra être suivis et manipulé par les propragateurs.
Les propagateurs
Les propagateurs sont des programmes écrits dans des langages comme Python et C. Ils utilisent l'interface de clingo pour accéder et modifier les assignations partielles et totales.
Les prochaines sections présenterons chacune un exemple de propagateur qui utilise cette interface pour implémenter un comportement que l'on aurait pas pu obtenir avec juste un code externe au solveur. Le premier propagateurs utilise très peu de notions de l'API, et les suivants augmenterons progressivement en complexité et complétude.
Exemple de propagateur : dot propagator
Celui-ci est très simple : il s'agit d'afficher un . pour chaque propagation du solveur, et d'en retirer un pour chaque backtrack (ou undo).
Cela résulte en une ligne de point qui progresse et régresse au fil de l'exploration du solveur.
Ce propagateur est présent dans le code source de clingo en figure d'exemple, et permet de toucher du doigt l'intérêt des propagateurs. Suis la version annotée des sources.
% Là on est dans le code ASP
#script (python)
# et paf, on est en python maintenant !
from time import sleep # pour donner une dimension humaine au programme
# La classe qui contient les méthodes.
# Notez qu'il n'y a évidemment aucune contrainte sur le nom,
# et surtout que la classe n'hérite de rien. Duck Typing FTW.
class Propagator:
# Première méthode : init
# (sans les `__`, car il s'agit bien de l'init du propagateur, pas de l'objet)
def init(self, init):
# init: un objet qui va nous donner des infos sur le solving
for atom in init.symbolic_atoms: # pour chacun des atomes du programme
init.add_watch(init.solver_literal(atom.literal)) # on le surveille
# atom.literal: la version littérale de l'atome, unique
# (contrairement aux littéraux du solveur).
# init.solver_literal: donne pour un littéral d'atome le littéral
# que le solveur utilise pour le référencer.
# init.add_watch: méthode qui permet d'ajouter un littéral à surveiller.
def propagate(self, ctl, changes):
# ctl: c'est le contrôleur du solving ; un objet qui mériterait
# une section à lui tout seul.
# changes: la liste des littéraux qui ont eu une assignation ;
# c'est eux qui nous intéressent.
for _ in changes: # la valeur exacte ne nous intéresse pas
print('.', flush=True, end='') # afficher un `.` sans passer à la ligne
sleep(0.1) # sans ça, on va rien voir, le programme semblera immédiat
# À essayer de votre côté : afficher changes à la place des points.
# Ça permet de voir en quoi consiste le backtrack.
def undo(self, solver_id, assign, undo):
# undo contient la liste des littéraux dont l'assignation est annulée.
# on va donc enlever un '.' pour chacune de ces assignation.
for _ in undo: # la valeur exacte ne nous intéresse pas
# D'abord, revenir en arrière avec \b,
# puis afficher un espace (effacer le point déjà affiché),
# puis revenir en arrière.
print('\b \b', flush=True, end='')
sleep(0.1) # sans ça, vous n'allez rien voir, le programme semblera immédiat
# notez que la function main est une convention de l'API de clingo :
# si elle existe, elle reçoit le contrôleur du solveur, et nous
# permet donc de contrôler tout le processus de solving.
def main(prg):
# prg: un contrôleur du solveur.
# d'abord, on enregistre une instance de notre propagateur
prg.register_propagator(Propagator())
# on ground le programme 'base', qui est le programme par défaut
prg.ground([("base", [])])
# on lance le solving
prg.solve()
print() # on écrit une ligne vide après les '.'
#end.
Vous pouvez (1) constater qu'il y a plus de commentaire que de code, et (2) tester ce code avec n'importe quel programme ASP. Le pigeon-hole problem est un bon candidat (pas un hasard qu'il soit fourni avec le propagateur) car il génère beaucoup de backtracks (de retours en arrière dans la recherche).
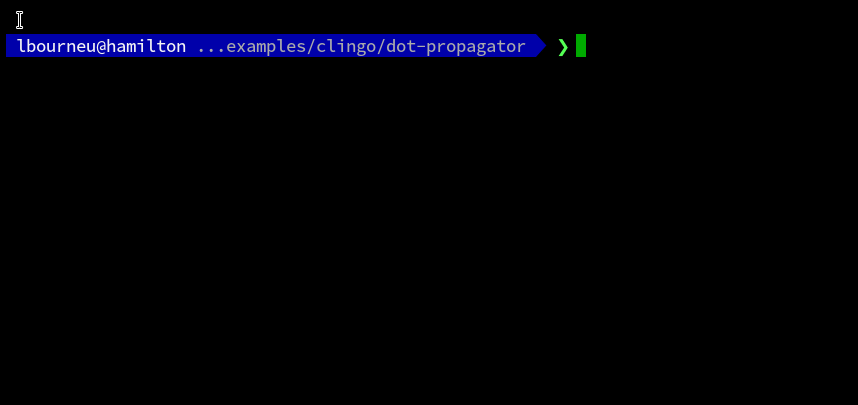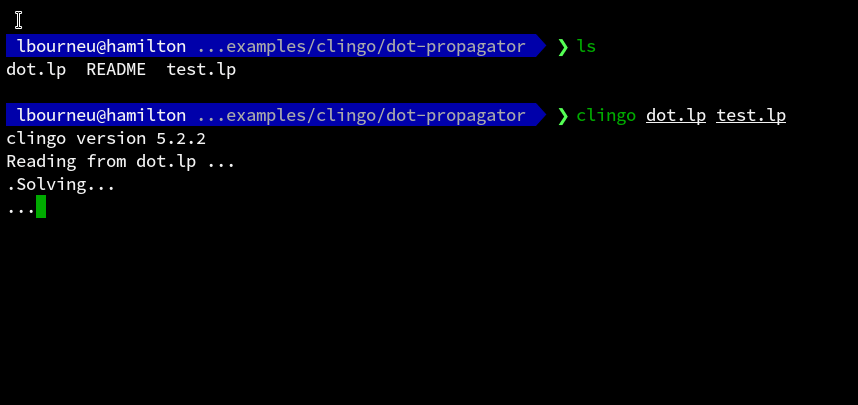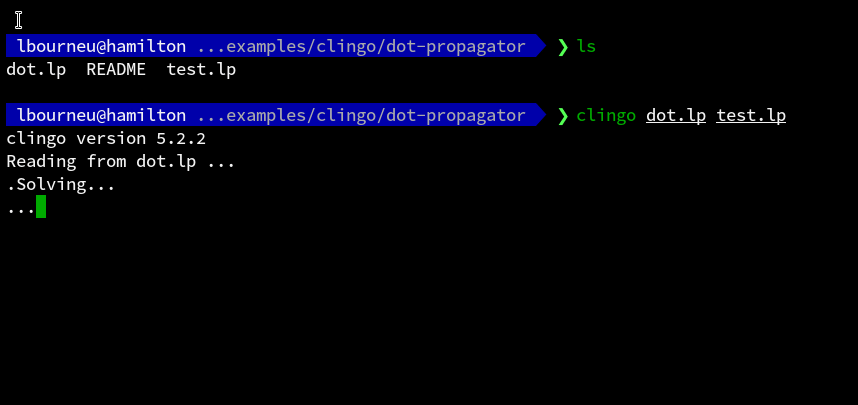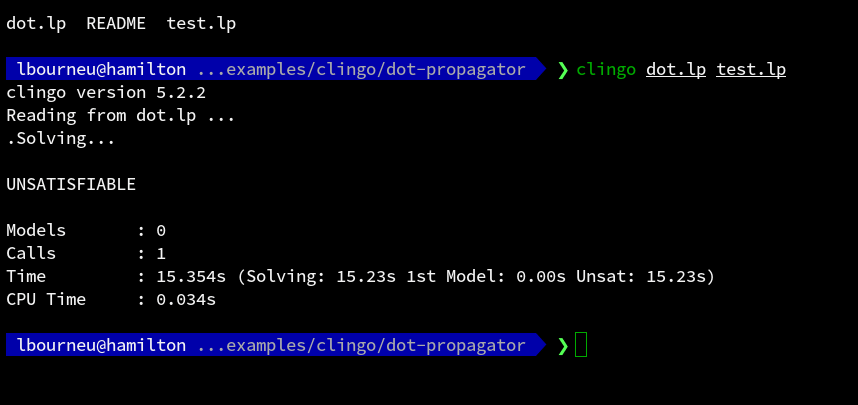
Le résultat est, vous vous en doutez, diablement rigolo :
Exemple de propagateur : color propagator
Dans la série des visualisations rigolotes, je vous propose… le color propagator !
Le principe : afficher les atomes du problèmes, et les mettre en couleur en fonction de leur valeur d'assignation.
Compliqué ? Non, pas tant que ça :
#script (python)
# de nombreux imports sont nécessaires
import os # pour nettoyer l'écran
import shutil # pour avoir la taille du terminal
import textwrap # pour afficher joliement les atomes
from time import sleep # pour que ça aille pas trop vite
import colorama # des couleurs dans le terminal ! (pip install colorama)
from colorama import Fore, Back
colorama.init() # nécessaire pour windows
# quelques constantes utiles
SPEED = 0.5
TERM_WIDTH = shutil.get_terminal_size().columns
def clear(): os.system('cls' if os.name == 'nt' else 'clear') # oui, c'est sale
# ça, ça va être notre classe propagateur. Notez que pour éviter de dupliquer
# du code, on a écrit une méthode `print_atoms` qui s'occupe
# d'afficher les atomes en couleur.
class ColorPropagator:
# appelée une fois au début: on va dire qu'on va observer tous les atomes du programme
def init(self, init):
self.sleep = SPEED
# On fait un dictionnaire pour se souvenir de la tête qu'à un atome,
# connaissant le littéral.
# Notez que les atomes qui sont soumis aux exactes même règles
# (et donc qui sont vrais ou faux en même temps) ont le même litéral.
# C'est pourquoi à un littéral (clef) on associe plusieurs valeurs
# (set d'atomes).
self.__symbols = {} # litéral du solveur -> set d'atomes
for atom in init.symbolic_atoms:
lit = init.solver_literal(atom.literal) # on récupère le litéral
init.add_watch(lit) # on veut être prévenu lorsque sa valeur de vérité change
if lit in self.__symbols: # on l'ajoute au dictionnaire
self.__symbols[lit].add(atom.symbol)
else:
self.__symbols[lit] = {atom.symbol}
# la fonction appelée quand un litéral surveillé change de valeur.
def propagate(self, ctl, changes):
# ctl: le contrôleur
# changes: la liste des litéraux qui ont changé de valeur
# C'est assez simple: on dit à print_atoms d'afficher tout ça
self.print_atoms(ctl.assignment, changes=changes)
def undo(self, solver_id, assign, undo):
# c'est globalement la même chose que propagate, juste avec un argument
# en plus qu'on utilise pas: solver_id.
self.print_atoms(assign, changes=undo)
# La fonction la plus complexe, qui n'a rien à voir avec les propagateurs
# en général.
def print_atoms(self, assignment, changes):
# assignment: objet qui peut donner pour chaque
clear() # on nettoie l'écran
to_print = ''
# là, on boucle sur chaque littéral et atomes associés
for idx, (lit, atoms) in enumerate(self.__symbols.items(), start=1):
# quand un litéral est associé à plusieurs atomes,
# on les affiche tous, séparés par un point-virgule
atom = ';'.join(map(str, atoms))
fore, back = Fore.WHITE, Back.BLACK # couleurs par défaut
# assignment.value renvoie, pour un littéral donné:
# - True si le littéral est vrai
# - False si le littéral est faux
# - None si le littéral n'a pas de valeur de vérité
if assignment.value(lit) is not None: # donc, là, il a une valeur de vérité
# s'il est vrai, on le met en vert (GREEN), sinon en rouge (RED)
fore = Fore.GREEN if assignment.is_true(lit) else Fore.RED
# si l'atome vient justement d'être changé, on le surligne en blanc
if lit in changes: back = Back.WHITE
elif lit in changes: # C'est un undo
# Effectivement, undo veut dire «enlever sa valeur de vérité à un atome»,
# donc, il ne passe pas la première condition. Mais il fait
# bien partie des atomes changé, donc on va le surligner aussi,
# mais en en bleu pour montrer que c'est un backtrack.
back = Back.BLUE
else: # et sinon, il n'a pas de valeur et n'a pas été changé
# on le laisse en couleur par défaut
pass
# maintenant on se prépare à l'afficher avec les couleurs sélectionnées
to_print += fore + back + atom + Fore.RESET + Back.RESET + ' '
# boucle terminée: on a généré toute la chaîne à afficher.
# pour rendre ça beau, on utilise textwrap et la taille de l'écran
# pour découper proprement les lignes.
print('\n\n' + '\n'.join(textwrap.wrap(to_print, width=TERM_WIDTH)))
# et on attend un poil, sinon on va rien voir.
sleep(self.sleep)
# Et voilà notre main, qui ressemble à un main des plus standards.
# Pas grand chose à dire dessus.
def main(prg):
prg.register_propagator(ColorPropagator()) # on y met notre propagateur
prg.ground([("base", [])]) # on grounde le programme de base
prg.solve() # et on résoud le problème !
# fin du python:
#end.
Le code réel est ici. Il n'est pas très différent, mais largement moins annoté.
Anecdote que-je-sais-pas-où-la-mettre : #count{}.% est le plus simple des débuts de ligne que j'ai trouvé pour faire un commentaire à la fois en ASP et en Python. En Python, toute la ligne est ignorée, et en ASP #count{} ne produit aucune règle. Il s'agit donc bien d'un commentaire pour les deux langages.
Exemple de propagateur : graphviz/dot propagator
Nous allons créer le propagateur qui permet de faire le dessin vu en introduction (avec les nœuds verts, les backtracks…).
Celui-ci est carrément plus haut niveau, non par sa complexité, mais parce qu'il génère un fichier dans un format nommé dot. Si vous ne connaissez pas le dot, sachez qu'il s'agit d'un format très utilisé pour décrire des graphes, au sens de la théorie des graphes.
La théorie des graphes et le dot sont tout à fait en dehors du scope de ce tuto, mais je vais essayer de faire court :
- un graphe, c'est un objet mathématique consistant en un ensemble de nœuds éventuellement reliés par des arêtes. C'est la structure de base en informatique, à partir de laquelle on dérive les autres. Les graphes sont utilisés dans tous les domaines : maths, physique, informatique évidemment, biologie, science sociales,… Vous en voyez souvent, sans vous en rendre compte (par exemple, l'image qui montre les propagations et backtracks du solveur au début de l'article).
- le dot, c'est une langue écrite, conçue par le projet graphviz, qui est aussi une suite logicielle. Les logiciels de graphviz sont capable de lire un programme en dot, et de générer une image ou d'autres fichiers qui représentent le graphe. C'est très puissant, car cela permet de voir graphiquement un graphe. C'est exactement ce qui nous intéresse.
Pour ce propagateur, nous allons donc exploiter le dot. L'idée est la suivante : un littéral est un nœud du graphe, et l'on trace un arc (une arête orientée, avec une flèche) du nœud 1 vers le nœud 2 lorsque qu'une propagation assigne une valeur au littéral 2, et que la précédente assignait le littéral 1. En d'autres termes, nous voulons visualiser le chemin emprunté par le solveur : dans quel ordre il assigne (et dé-assigne) les atomes/littéraux.
Le résultat est de facto très visuel : on génère des visualisations de graphes avec dot !
Le graphviz/dot propagator
Le code est disponible sur son dépôt, et reproduit ci-après avec des annotations supplémentaires :
#script(python)
class DotPropagator:
"""A non-literal *dot* propagator"""
# Cette fois-ci, notre classe est un poil plus complexe.
# Elle a un __init__, qu'on utilise pour préparer les conteneurs et le fichier dot
def __init__(self, dotfiledesc:str):
# dotfiledesc -- un descripteur de fichier dans lequel on peut écrire
self.__dotfiledesc = dotfiledesc
self.__stack = ['Start'] # c'est une pile de nœuds
self.__step = 0 # pour pouvoir annoter les arcs
self.__stable_nodes = set() # tous les nœuds stables
self.write_header() # on commence par écrire des lignes obligatoires
# C'est bon ! l'objet est prêt à faire propagateur !
def init(self, init):
# exactement comme pour notre premier propagateur: on suit tous les atomes
self.__symbols = {} # littéral -> set d'atomes
for atom in init.symbolic_atoms:
lit = init.solver_literal(atom.literal)
init.add_watch(lit)
if lit in self.__symbols: # on l'ajoute au dictionnaire
self.__symbols[lit].add(atom.symbol)
else:
self.__symbols[lit] = {atom.symbol}
def propagate(self, ctl, changes):
# ctl: l'objet de contrôle du solveur
# changes: les littéraux qui ont reçu une valeur
level = ctl.assignment.decision_level
self.__step += 1
# pour chaque changement, on va écrire dans le fichiers dot.
for lit in changes:
self.write('\t{} -> {} [label="{}"];'.format(self.last_node, lit, self.__step))
self.push_node(lit) # et on ajoute le litéral dans la pile
def undo(self, sid, assign, undo):
# sid: on s'en fiche
# assign: ce sont les assignations de valeurs de vérité, on s'en fiche aussi
# undo: les litéraux qui ont été changés
template = '\t{} -> {} [style=dotted label={}];'
while undo: # tant qu'il y a un nœud dans les undo
prev_node = self.pull_node() # on récupère le sommet de la pile
assert prev_node in undo # par construction, il appartient aux nœuds retirés
# On affiche le backtrack en dot avec une flèche en pointillé
# qui retourne sur le nœud actuel (la tête de pile).
self.write(template.format(prev_node, self.last_node, self.__step))
undo.remove(prev_node) # on enlève le littéral de la liste des undo
def check(self, ctl):
# Le solveur trouve que l'assignation est totale et valide :
# il s'apprête à générer l'answer set !
# Que faisons-nous ? On marque le nœud courant comme tel.
self.__stable_nodes.add(self.last_node)
# Méthodes pour modifier le nœud courant (le sommet de la pile)
def pull_node(self): # le nœud courant devient le précédent
*self.__stack, ret = self.__stack
return ret
def push_node(self, uid): # nouveau nœud courant !
self.__stack.append(uid)
@property
def last_node(self): # juste un raccourcis pour le nœud courant
return self.__stack[-1]
def write(self, line): # pour écrire du dot
self.__dotfiledesc.write(line.rstrip() + '\n')
def write_nodes(self): # pour écrire les nœuds
for uid, atoms in self.__symbols.items():
self.write('\t{} [label="{}"{}];'.format(
uid, ' '.join(str(atom) for atom in atoms),
' fillcolor="green"' if uid in self.__stable_nodes else ''
))
# Deux méthodes pour les premières et dernières lignes du dot,
# qui sont toujours les mêmes.
def write_header(self):
self.write('digraph solving {')
self.write('\tgraph [dpi=400];') # bonne résolution
self.write('\tnode [style=filled];') # affiche la couleurs de fond
self.write('\tedge [arrowsize=0.5];') # flèche plus petites
def finalize(self):
self.write_nodes()
self.write('}')
# Le main est assez standard également,
# sauf le fait que l'on fait tout le solving avec un fichier ouvert,
# que l'on donne à notre propagateur.
def main(prg):
with open('out.dot', 'w') as fd:
propagator = DotPropagator(fd) # c'est notre propagateur !
prg.register_propagator(propagator) # on l'enregistre
prg.ground([("base", [])]) # on ground
prg.solve() # on solve
propagator.finalize() # et on termine d'écrire le dot
#end.
Utiliser le propagateur graphviz/dot
Le code va générer un fichier out.dot. Avec graphviz, ou tout autre logiciel qui gère le format DOT,
vous pouvez afficher le résultat comme une image.
Si vous réutilisez le code du pigeon-hole problem vu plus haut, vous verrez que le graphe généré est un gros sac de nœud (qu'est-ce qu'on rigole !).
Avec le code suivant :
a;b.
c;d:-a.
e;f:-b.
Vous verrez quelque chose de beaucoup plus simple, que vous avez déjà vue plus haut :

Quelques questions pour le lecteur attentif :
- que se passe-t-il si on ne demande qu'un seul answer set au solveur ?
- que se passe-t-il si deux choix différents peuvent décider la valeur d'un seul atome ?
- et donc, dans quels cas le graphe généré est-il un arbre ?
Écrire des contraintes en Python
Les contraintes, on s'en souvient : ce sont ces expressions très utiles qui permettent d'écarter un modèle s'il ne réponds pas à certains critères.
L'objectif ici est de pouvoir, simplement, écrire des contraintes en Python plutôt qu'en ASP.
Le rationnel est simple : une contrainte en ASP est intégralement traduite durant le grounding, ce qui peux coûter très cher si elle utilise beaucoups de variables. Par exemple, si vous voulez vérifier que deux variables conservent une dépendance particulière (l'une plus grande que l'autre, par exemple), la contrainte devra énumérer tous les cas possibles, c'est-à-dire toutes les combinaisons des valeurs de variables : la complexité en mémoire est quadratique.
Il n'existe pas de moyen pour dire au solveur «ne grounde pas cette contrainte, mais évalue-la pendant le solving», ce qui serait peut-être moins rapide, mais clairement moins coûteux en mémoire.
D'où l'intérêt d'écrire les contraintes à l'aide d'un propagateur : le propagateur travaille en même temps que le solveur, sans être limité par lui.
Cette section s'intéresse en fait à une fonctionnalité de clyngor, mon module surcouche à l'API officielle. Clyngor propose dans son API un moyen simple pour faire des contraintes en ASP :
#script(python)
from clyngor import Constraint, Variable as V, Main
# On définit la contrainte
def formula(inputs):
# inputs: c'est un dictionnaire qui mappe un atome avec sa valeur de vérité (True/False)
# on retourne si oui ou non on écarte le modèle.
# ici, si le modèle contient b(2), on l'écarte
return inputs[('b', (2,))]
# On l'encapsule dans l'objet dédié, qui est en fait un propagateur
constraint = Constraint(formula, {('b', (V,))})
# On lance le grounding et le solving, avec le propagateur enregistré
main = Main(constraint)
#end.
b(1);b(2);b(3). % choisi l'un des trois
Les résultats attendus sont les suivants :
Answer 1:
b(1)
Answer 2:
b(3)
Réalisation
Je ne vais pas s'amuser à annoter tout le code de clyngor, mais plus précisément celui de l'objet PyConstraint qui implémente le comportement. Ici, ce sera juste l'occasion de voir comme cette merveilleuse API fonctionne under the hood.
Ce sera l'occasion de voir un autre propagateur, ainsi l'usage des clauses pour modifier l'exploration de l'espace de recherche.
Voici donc le code de la classe et des fonctions/objets qu'elle utilise (légèrement simplifié pour ignorer les détails dû à l'API de clyngor) avec le code d'exemple ; il ne vous reste plus qu'à copier-coller ça dans un fichier :
#script(python)
from collections import defaultdict
Variable = ... # Ellipsis en Python
# La fonction qui suit sert à transformer un argument d'atome,
# sous la forme d'une instance de la classe clingo.Symbol,
# en objet purement python (listes, tuples, int,…).
# Cette fonction est en réalité plus complexe,
# car elle doit gérer les structures récursives,
# les types non standards de clingo (comme #inf et #sup),
# et les double quotes dans les strings.
# le code complet est ici :
# https://github.com/Aluriak/clyngor/blob/impl/propagator/clyngor/utils.py#L56
def clingo_value_to_python(obj:int or str or 'Symbol'):
if isinstance(obj, (int, str)):
return obj
if type(obj).__name__ == 'Symbol':
typename = str(obj.type).lower()
if typename == 'string':
return '"' + obj.replace('"', '\\"') + '"'
if typename == 'number':
return int(str(obj))
raise TypeError("Can't handle values like {} of type {}."
"".format(obj, type(obj)))
# La classe qui implémente le comportement complet
class Constraint:
# Le constructeur de la classe : on prend une formule
# et les atomes qui doivent être suivis.
def __init__(self, formula:callable, inputs:[tuple]):
self.__formula = formula
# les inputs peuvent être données de différentes manières :
# - comme des strings, e.g. 'a(2,3)'
# - comme des tuple, e.g. ('a', (2, 3))
# la seconde est plus lourde, mais n'oblige pas de donner
# les valeurs exactes des arguments, e.g. ('a', (V, 3))
self.__inputs = frozenset(inputs)
# on sauvegarde donc les versions string et tuple à part
self.__str_inputs = frozenset(input for input in self.__inputs
if isinstance(input, str))
self.__raw_inputs = frozenset(input for input in self.__inputs
if not isinstance(input, str))
# la fonction de propagateur d'initialisation
def init(self, init):
# on a un dictionnaire qui nous permet de connaître, pour un littéral de solveur,
# l'atome dans sa version string ou tuple.
self.__symbols = defaultdict(set)
# pour chacun des atomes, il faut décider si on veux le suivre ou pas
# (en se basant sur les inputs récupéré dans le constructeur)
for atom in init.symbolic_atoms:
lit = init.solver_literal(atom.literal)
# d'abord on teste l'atome lorsque représenté comme une string
repr_str = str(atom.symbol)
if self._match_str(repr_str): # vrai si repr_str est attendu par la formule
init.add_watch(lit)
self.__symbols[lit].add(repr_str)
continue
# et ensuite, on le teste sous le format raw
repr_args = tuple(map(clingo_value_to_python, atom.symbol.arguments))
repr_raw = atom.symbol.name, repr_args
if self._match_raw(*repr_raw): # idem que self._match_str, mais avec Variable
init.add_watch(lit)
self.__symbols[lit].add(repr_raw)
# fonction appelée quand une propagation est réalisée
def propagate(self, ctl, changes):
# on appelle la formule donnée par l'utilisateur, avec en argument un dictionnaire
# qui mappe la représentation d'un atome et sa valeur de vérité.
fulfilled = self.__formula({
repr: ctl.assignment.value(lit)
for lit, reprs in self.__symbols.items()
for repr in reprs # plusieurs atomes peuvent avoir la même valeur de littéral
})
# si la contrainte est remplie, on invalide le modèle
if fulfilled:
self.__invalidate_model(ctl)
def __invalidate_model(self, ctl):
# On ajoute, si c'est pas encore fait, un nouveau littéral.
# C'est un peu comme si on ajoutait un atome,
# mais sans lui donner de représentation comme a(2) par exemple.
self.__added_lit = ctl.add_literal()
# Les deux lignes suivantes servent à ajouter une «clause»,
# indiquant que notre nouveau littéral est vrai.
# Quand on ajoute une clause, il se peut que le solveur
# ait besoin de revérifier l'espace de recherche.
# Dans notre cas, on ne le change pas puisque le littéral assigné est tout nouveau
# et est indépendant du programme ASP.
# Mais dans le cas général, on pourrait assigner la valeur d'un atome existant,
# et donc là le solveur devrait réagir en conséquence.
if not ctl.add_clause([self.__added_lit]) or not ctl.propagate():
return
# C'est là que la magie se passe : on dit que le littéral est faux.
if not ctl.add_nogood([self.__added_lit]) or not ctl.propagate():
return
# Ce qui entre en conflit avec la clause précédente, qui le déclarait vrai.
# La situation est donc instable,
# aucun modèle ne pourra être vrai dans ces conditions !
# Les fonctions suivantes sont des détails d'implémentation,
# et n'ont pas grand chose à voir avec les propagateurs,
# mais je les laisse là pour la complétude du code.
def _match_str(self, atom:str) -> bool:
# Retourne vrai si l'atome en string donné
# est dans les inputs attendues par la formule.
if atom in self.__str_inputs:
return True
def _match_raw(self, name:str, args:tuple) -> bool:
# Retourne vrai si l'atome en tuple donné
# est dans les inputs attendues par la formule.
# Premier cas : pas de Variable dans le tuple.
if (name, args) in self.__raw_inputs:
return True
# Second cas : il y a des Variable dans le tuple.
for pred, params in self.__raw_inputs:
if pred == name and len(args) == len(params):
# C'est le même prédicat et le même nombre de variable
# donc c'est peut-être bon…
for arg, param in zip(args, params):
# Deux cas : soit l'argument est une Variable,
# soit c'est celui attendu.
if param is Variable or arg == param:
return True
# On implémente la contrainte
def formula(inputs):
# c'est équivalent à `:- b(2).`
return inputs[('b', (2,))]
# On lance le grounding et le solving, avec le propagateur enregistré
def main(prg):
constraint = Constraint(formula, {('b', (Variable,))})
prg.register_propagator(constraint)
prg.ground([("base", [])])
prg.solve()
#end.
% un code ASP qui génère 1 parmi b(1..3).
1{b(X): X=1..3}1.
Avec ce code complet et fonctionnel, les modèles de sortie seront bien b(3) et b(1).
Notez que l'objet Contrainte réalise les vérifications à chaque propagations.
Il est possible de ne les enclencher que sur les check, en changeant def propagate(self, ctl, changes): par def check(self, ctl):.
Avec ce changement, la contrainte sera vérifiée seulement lorsqu'un modèle sera prêt à être envoyé ;
il s'agit donc moins de guider le solveur que de contrôler les sorties.
Conclusions
C'était une grosse (quête) annexe, avec beaucoup de code (et hélas, pas en ASP). Mais c'est un mal pour un bien : l'interface des propagateurs est un outils extrêmement puissant pour travailler avec le solveur. En effet, jusqu'alors, on déléguait au solveur des questions. Maintenant, nous avons un moyen de dialoguer avec lui pendant ses recherches pour l'aider, ou contrôler finement l'exploration de l'espace de recherche.
Dans les applications évidentes, on trouve les «observateurs», qui regardent comment se passent le solving et propose un rendu en conséquence. On trouvera aussi toutes les notions rigolotes relatives aux contraintes dynamiques, ou plus généralement l'appel à des sources extérieures pour résoudre des propagations ou valider les modèles.
D'autres quêtes annexes viendront, pour apporter d'autres applications aux propagateurs, ou montrer d'autres manières d'étendre ASP.
Enfin, maintenant que vous avez les bases, je vous recommande clyngor, ne serait-ce que pour y jeter un œil. Ce package propose quelques aides pour les propagateurs, l'API générale de clingo et l'appel de ce dernier dans python. En un mot, c'est une surcouche à l'API officielle. Il propose aussi une implémentation complète de PyConstraint que nous avons détaillé dans la dernière section.