Ceci est une aventure dans le domaine du calcul quantique (réalisé avec un ordinateur quantique). Je n'ai aucune expertise dans ce domaine, mes seules connaissances viennent de quelques vidéos et articles, mais surtout de tripatouillages têtus réalisés à tâton, lors de mon utilisation du quantum experience d'IBM, qui propose une interface web programmable pour simuler un ordinateur quantique (et qui permet aussi de faire tourner le code sur un vrai ordinateur quantique !).
Pour une bonne introduction au principe d'ordinateur quantique, allez voir cette vidéo de ScienceÉtonnante.
Mise en place et bases
Rien à installer (mais il faut s'inscrire), c'est une page web sur laquelle nous pouvons coder. Le code fait, il est possible de le simuler, ou de le calculer.
Le simulateur est probablement un gros calculateur installé sur site, vu que mon PC ne semble pas faire de calcul pendant la simulation. Son usage n'est pas limité, et consiste en un ordinateur normal (binaire) qui simule le comportement d'un ordinateur quantique. Il est possible de choisir le nombre de reproductions (plus c'est grand, plus le résultat est statistiquement valide) ainsi que la seed, c'est-à-dire la valeur de départ pour les choix pseudo-aléatoires.
À l'inverse, le calcul réel fait appel à l'ordinateur quantique de 5 bits, et est évidemment en accès limité (on a droit à un certain nombre de runs par jour et par compte), et géré par un système de queue, pour éviter que quelqu'un ne monopolise la machine. Mais, l'ordinateur quantique étant ce qu'il est, le résultat est bien celui que l'on veut, pas juste une simulation.
Je me contenterais de jouer ici avec la simulation, c'est tout ce que je demande.
langages de programmation
Ici, le langage de programmation est le QASM, développé par IBM spécifiquement pour cette application. La réflexion sur les langages de programmation pour ordinateur quantique n'est pas nouvelle, et elle est le centre de beaucoup d'intérêt, car la création d'un langage adapté aux problème que l'ordinateur peut résoudre est la clef pour une informatique efficace.
Notez le côté «automate à pile» du langage, qui me laisse à penser que si un futur où les Quantum Processing Unit se placent à côté des Graphical Processing Unit dans les configurations minimales nécessaires pour les jeux vidéos, on verra naître des langages très haut niveau qui pourrait permettre de mixer la programmation binaire, et quantique comme aujourd'hui avec la binaire et graphique avec des langages comme OpenGL.
Notez également que chaque porte est associée à trois description : une avec du texte, la décrivant pour les non-matheux comme moi, une en QASM, et une en matrice. Les trois formulations sont théoriquement équivalentes.
dualité visuel/source
Notons que pour QASM, il existe deux manières de représenter le langage : graphique (avec les carrés colorés) et textuelle (comme un bon code source bien standard). Je vais rester sur le graphique, le textuel étant réservé à ceux qui comprennent ce qu'ils font…
Premiers pas
qubit
Un qubit, c'est un objet assez complexe qu'on peut représenter comme une sphère de Bloch :
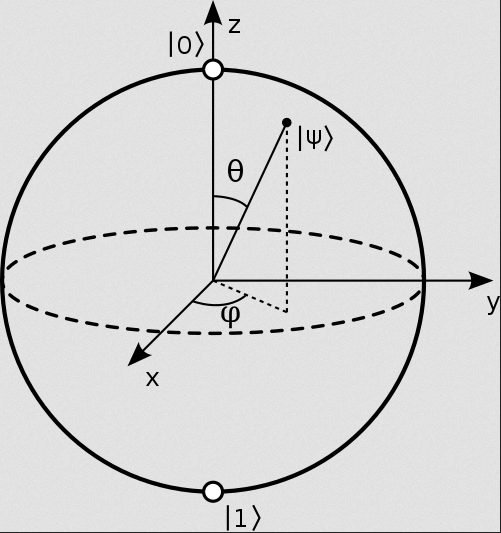
Ok, ça a l'air chiant, ça rappelle des cours de trigonométrie. Effectivement, c'est lié, mais c'est pas le plus important.
Donc, une sphère de Bloch, c'est une sphère, donc trois dimensions, X, Y et Z. Par convention, on dit que Z porte l'information binaire : ainsi, être tout en haut de la sphère (donc 1 en Z, et zéro en X et Y) est équivalent à la valeur binaire 0, et être tout en bas (-1 en Z, zéro en X et Y) est équivalent à la valeur binaire 1. Voilà, on vient d'utiliser une sphère de Bloch pour modéliser le calcul binaire ! On pourrait s'amuser à refaire toute la théorie derrière le calcul non quantique avec des sphères de Bloch, mais l'intérêt serais limité.
Vous devinez que ce qui nous intéresse, c'est ce qu'il y a entre le point le plus haut (donc, 1 en Z, et zéro en X et Y) et le point le plus bas (-1 en Z). En fait, à un instant donné, un qubit est en fait un point sur cette sphère.
Pour symboliser un point sur une sphère, ya plein de méthodes. Nous, on va utiliser les axes X, Y et Z pour se repérer, mais on va aussi voir l'usage de ϴ (thêta) et Φ (phi), qui sont deux angles indiquant la position du qubit sur la sphère (regardez encore la sphère de Bloch, et le principe de coordonnées sphériques), ϴ indiquant l'angle à l'axe Z et Φ l'angle à l'axe X. L'angle à l'axe Y se déduit des deux précédents.
La question est donc : «que symbolise le fait qu'un qubit soit pas sur une extrémité de l'axe Z ?». La réponse est simple : c'est une probabilité, induite par une superposition d'état. En réalité, quand un qubit est en haut, il ne dit pas «ma valeur est 0», mais plutôt «dans 100% des cas, ma valeur est 0». Ah ! Intuitivement, ça veut dire que quand on est à mi-chemin des deux pôles (donc, sur l'équateur, par exemple à X=1 et Y=Z=zéro), ça veut dire que mon qubit indique qu'il y a 50% de chance d'être à 1, et 50% d'être à 0. On note ça ainsi : 0.5×1 + 0.5×0. À l'inverse, se situer au sommet de l'axe Z s'écrit 1×1 + 0×0. Donc, pour donner une probabilité différente à notre qubit, il suffit de le déplacer selon l'axe Z (qu'on pourrait nommer également la latitude, si on continuait l'analogie avec la Terre).
Donc, maintenant que l'on sait qu'un qubit c'est un point sur une sphère qui représente une probabilité d'obtenir 0 ou 1, on peut se poser la question : «on peut en faire quoi ?» Eh bien, accrochez-vous à vos siège : c'est là qu'on va passer par des portes (au sens de porte logique, hein).
La porte d'Hadamard
La porte d'Hadamard est une excellente manière d'expliquer le principe de base du calcul quantique, car en général, voici ce qu'on dit d'elle : «la porte d'Hadamard change un qubit de valeur 1×0 + 0×1 en qubit de valeur 0.5×0 + 0.5×1».
En d'autres termes, si vous avez un qubit qui est au sommet de l'axe Z (pôle nord), si vous le passez dans la porte d'Hadamard, il va se retrouver sur le cercle au milieu (l'équateur). Bon, le problème avec cette définition, c'est qu'elle est imprécise : quel point de l'équateur ? N'importe lequel ? Comment se comporte la porte sur un qubit qui n'est pas au sommet de l'axe Z ?
Déjà, regardons ce qui se passe lorsque je simule un ordinateur quantique avec un qubit sur lequel j'applique la porte d'Hadamard :
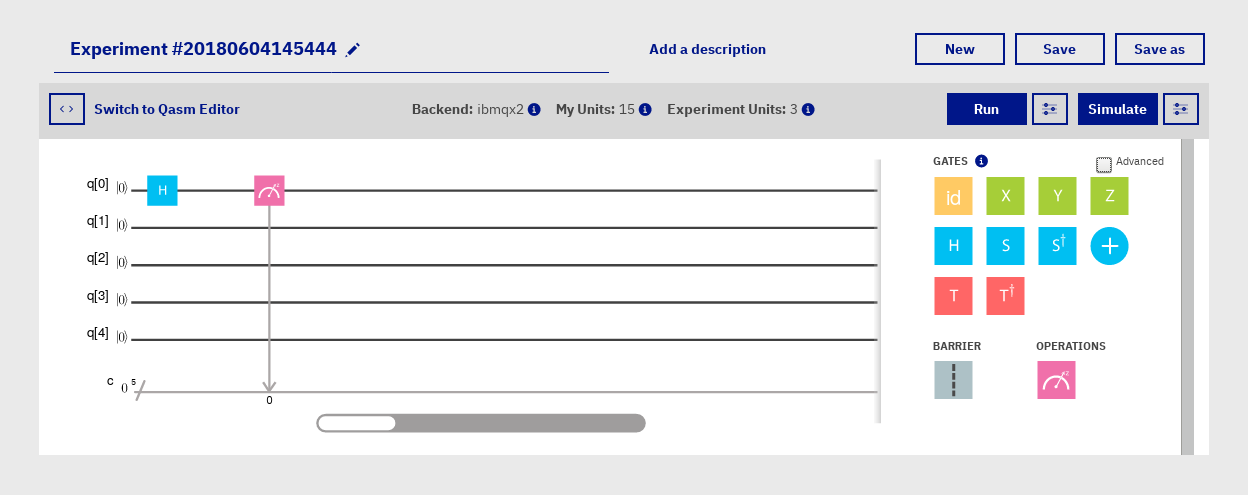
On voit ici que j'applique la porte d'Hadamard (le carré bleu avec un H) sur le qubit numéro 0, et ensuite je l'affique (carré rose). Je lance la simulation, et voici :
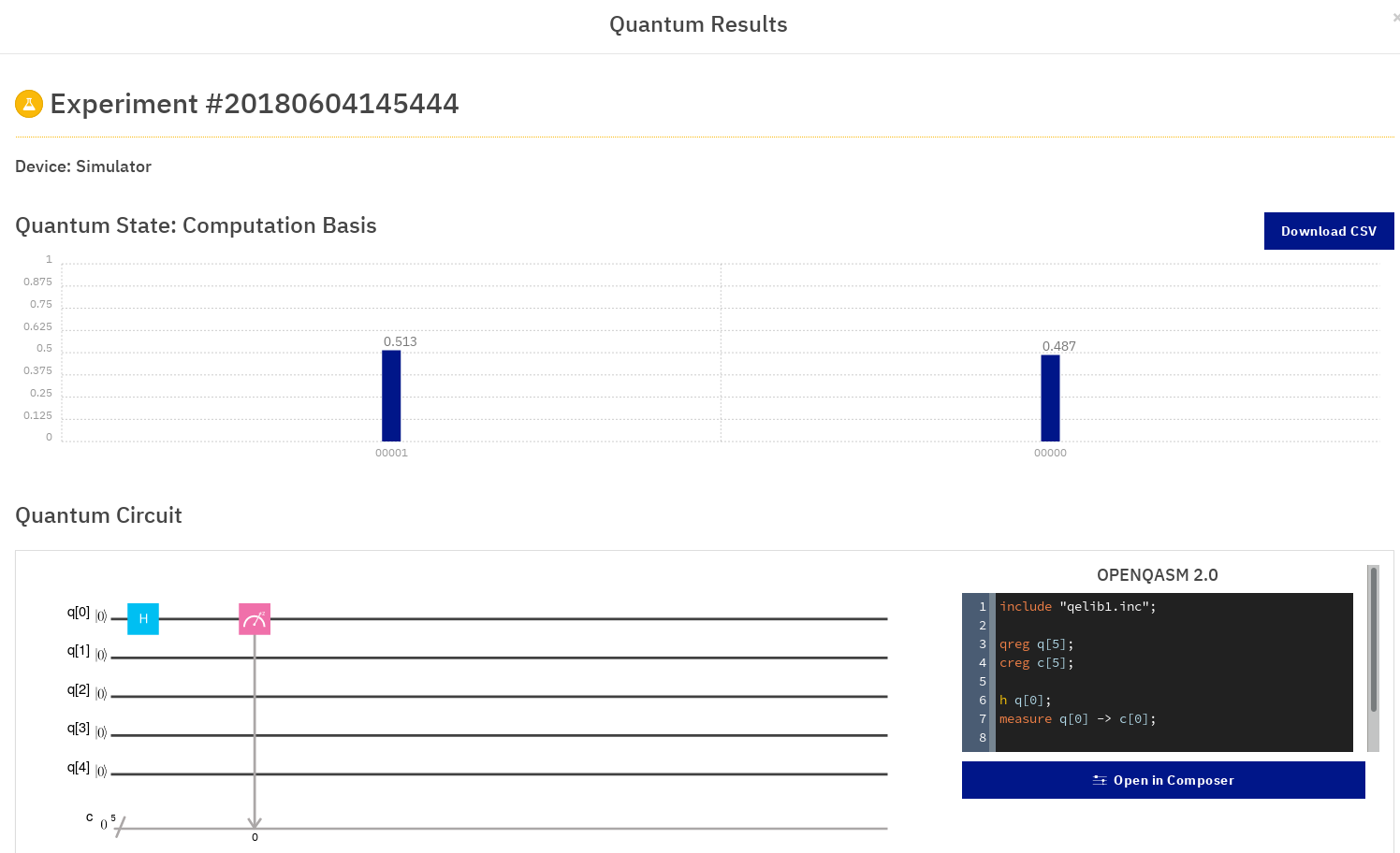
Nous voyons deux barres bleue, d'à peu près la même taille. Elles indiquent les proportions de combinaisons de qubit obtenus. Ici, puisque 4 des 5 qubits ne sont pas touchés, ils sont à zéro (valeur de base, mise par défaut par l'interface, c'est-à-dire que ϴ=Φ=zéro, c'est un choix arbitraire). Il n'y a donc que deux possibilités : soit le cinquième qubit est à 1, soit il est à 0. Hors, grâce à la porte d'Hadamard, nous avons fait en sorte qu'il soit à 1 dans 50% des cas. C'est pour cette raison que les deux proportions (0.513 et 0.487) sont si proches : sur les 1000 runs, le simulateur à compté 513 qubit à 1 lorsqu'il a été lu, et 487 à zéro. Si on augmente le nombre de tirs/shots, on augmente l'échantillon et par conséquent on se rapproche d'un 50-50 parfait.
Bon, ok, mais du coups : elle fait quoi exactement la porte d'Hadamard dans d'autres cas ? Eh bien, en réalité, cette porte, ainsi que toutes les portes logiques en calcul quantique, réalise une rotation du point sur la sphère.
Et la rotation de la porte d'Hadamard est très simple : X devient Z, et Z devient X. Regardez encore la sphère de Bloch, placez un point au pôle nord, et échangez les valeurs de X et Z. Que se passe-t-il ? Le point est maintenant au sommet de l'axe X. Réappliquez encore la même transformation, et le point revient au pôle nord. En d'autres termes, appliquez deux fois la porte d'Hadamard sur un qubit de valeur 0, et il sera encore à 0. Testez avec l'interface, vous verrez, c'est exactement ce qui se passe.
Wait, what ?
Ce qu'on vient de faire ici, c'est de comprendre un truc primordial : les portes logiques ne servent qu'à déplacer des qubit sur la sphère de Bloch. Quand on nous dit que la porte d'Hadamard nous permet de passer de 1×1 + 0×0 à 0.5×1 + 0.5×0, c'est comme dire un sceau remplit de plomb, ça coule. C'est vrai, mais ce n'est pas toute la vérité. En exprimant la porte comme une rotation, nous pouvons comprendre son effet sur n'importe quel qubit.
Notez le parallèle avec le calcul binaire : les portes logiques comme OR et AND permettent de placer un bit à la valeur 0 ou à la valeur 1. En fait, ces portes logiques renvoient une position dans la sphère de Bloch, en s'appuyant sur la valeur d'autres bits. Mais quoi qu'il arrive, dans un calcul binaire, il n'existe que deux positions valides dans la sphère de Bloch : 1×1 + 0×0 ou 0×1 + 1×0.
Note sur le quantique
Notez que dans la théorie quantique, quand on dit qu'un qubit est dans un état superposé, genre 0.7×1 + 0.3×0, c'est que l'on ne sait pas ce qui va être choisi, mais juste la probabilité. Si l'on mesure (avec la porte rose de mesure dans l'interface), on ouvre la boîte et on regarde. La valeur est fixée.
Autre opérations basiques
Voici une nouvelle simulation : j'applique trois transformations différentes à trois qubits, indépendamment les un des autres :
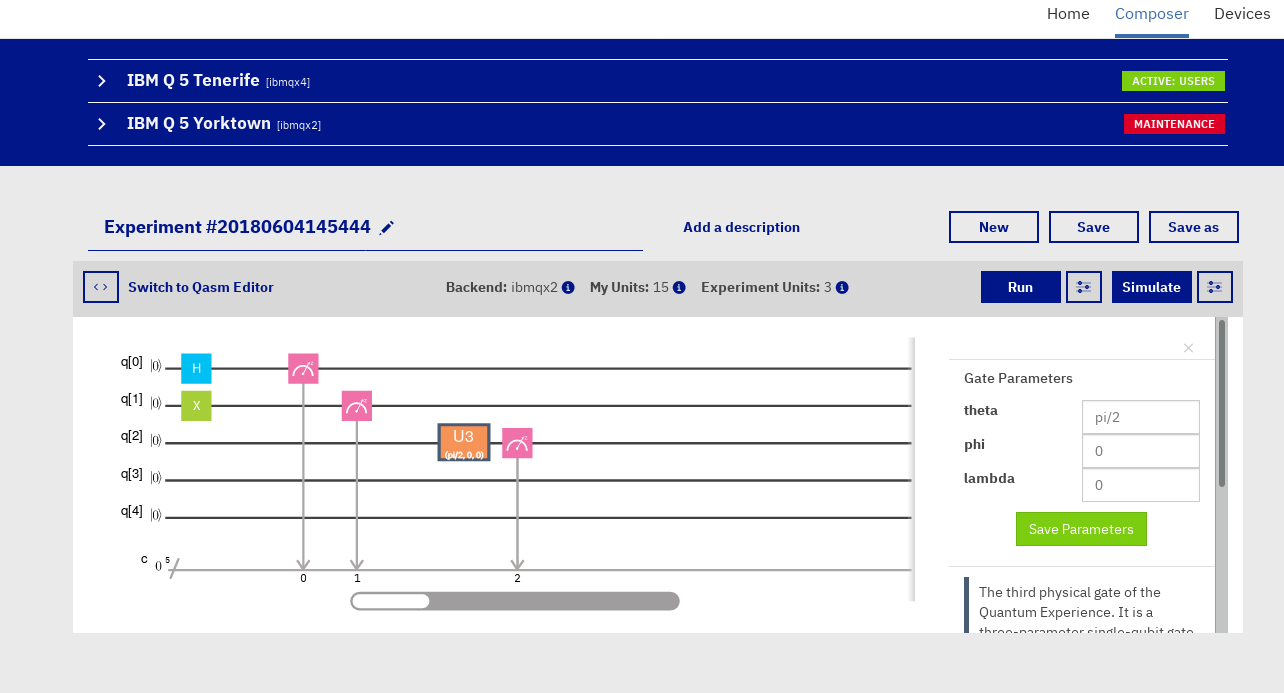
La première, nous venons de la voir, c'est la porte d'Hadamard. Les suivantes font appel à de nouvelles portes. La seconde (sur la ligne q[1]), c'est la rotation de pi sur l'axe X, aussi appelée rotation de Pauli X. En clair, vous prenez la sphère sur l'axe X, et vous la faite tourner autour de cet axe de pi (un demi-cercle). Si votre point/qubit était au pôle nord, alors il va finir au pôle sud. Autrement dit, la valeur attendue pour le second qubit est 1 dans 100% des cas, soit 1×1 + 0×0.
Le troisième qubit est quant à lui modifié avec une porte à triple argument, où l'on peut donner theta, phi et lambda (comme montré à droite, dans l'interface de choix des valeurs des variables). Je n'ai donné que theta, et je lui ai donné la valeur de pi/2, soit un quart de cercle. Comme montré dans la sphère de Bloch, theta est l'angle avec l'axe Z. En le mettant au quart de cercle, et en mettant phi à un angle de zéro, je fait effectuer au qubit une rotation qui va le placer… au sommet de l'axe X. (Notez que je n'ai pas parlé de lambda : c'est normal, j'ai aucune idée de ce que c'est. Peut-être l'angle avec Y, mais ça me semble bizarre)
Et lorsque je lance la simulation avec 1000 tirs, j'obtiens :
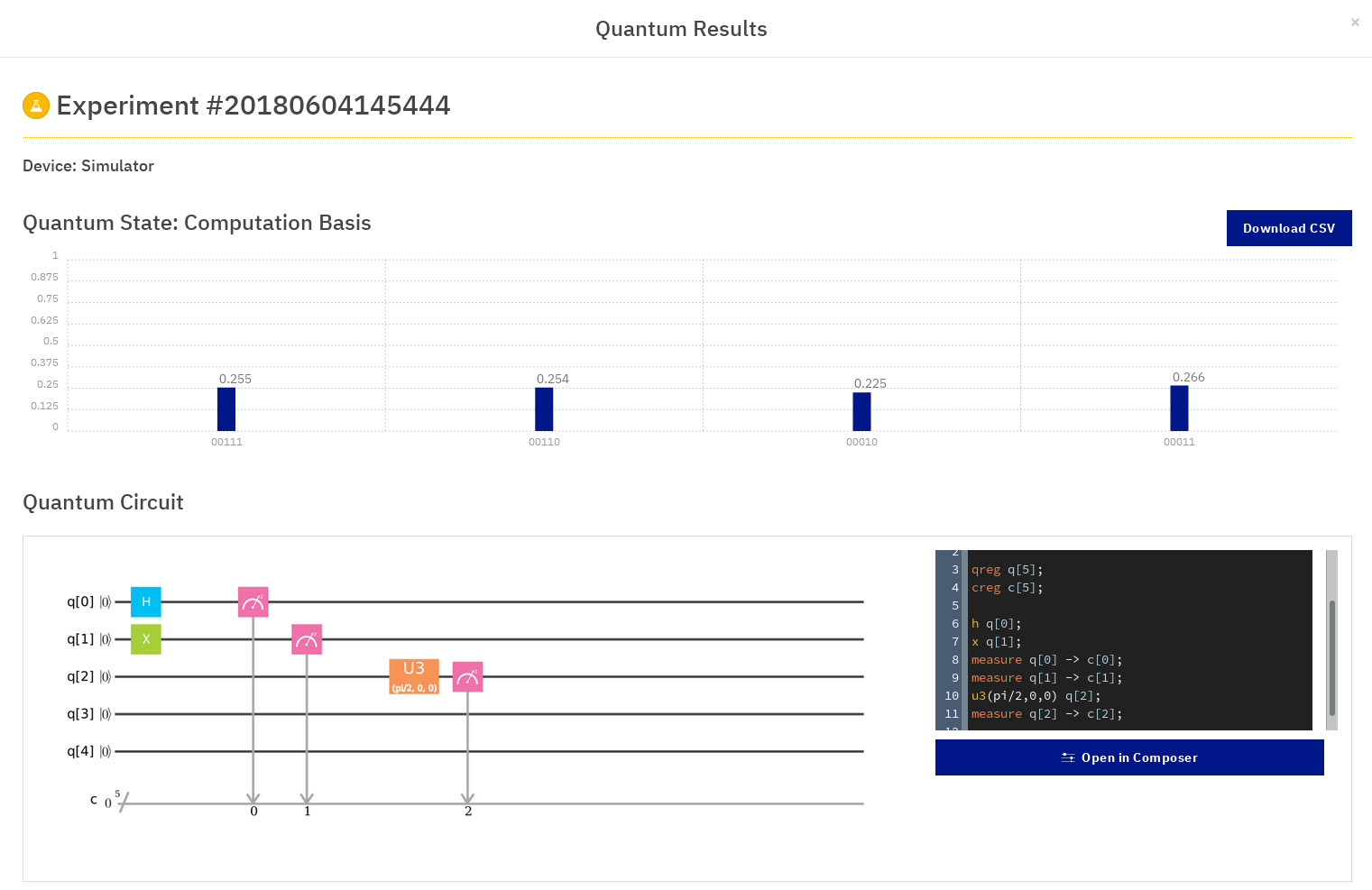
Ah ! Vérifions que notre théorie sur le fonctionnement de l'ordinateur quantique fonctionne : tout d'abord, nous nous attendions à avoir toujours 1 pour le second qubit (en partant de la fin), et effectivement, les quatre solutions sont bien toutes avec ce qubit à 1. Maintenant, les deux autres qubit sont libres de choisir, en équiprobabilité. Nous devrions donc avoir quatre valeurs différentes avec un nombre d'occurence proche, donc 25% chacunes. C'est exactement ce qu'on observe !
Maintenant, relançons la simulation, mais avec un peu moins de pi/2, par exemple 1 tout rond, comme valeur pour theta :
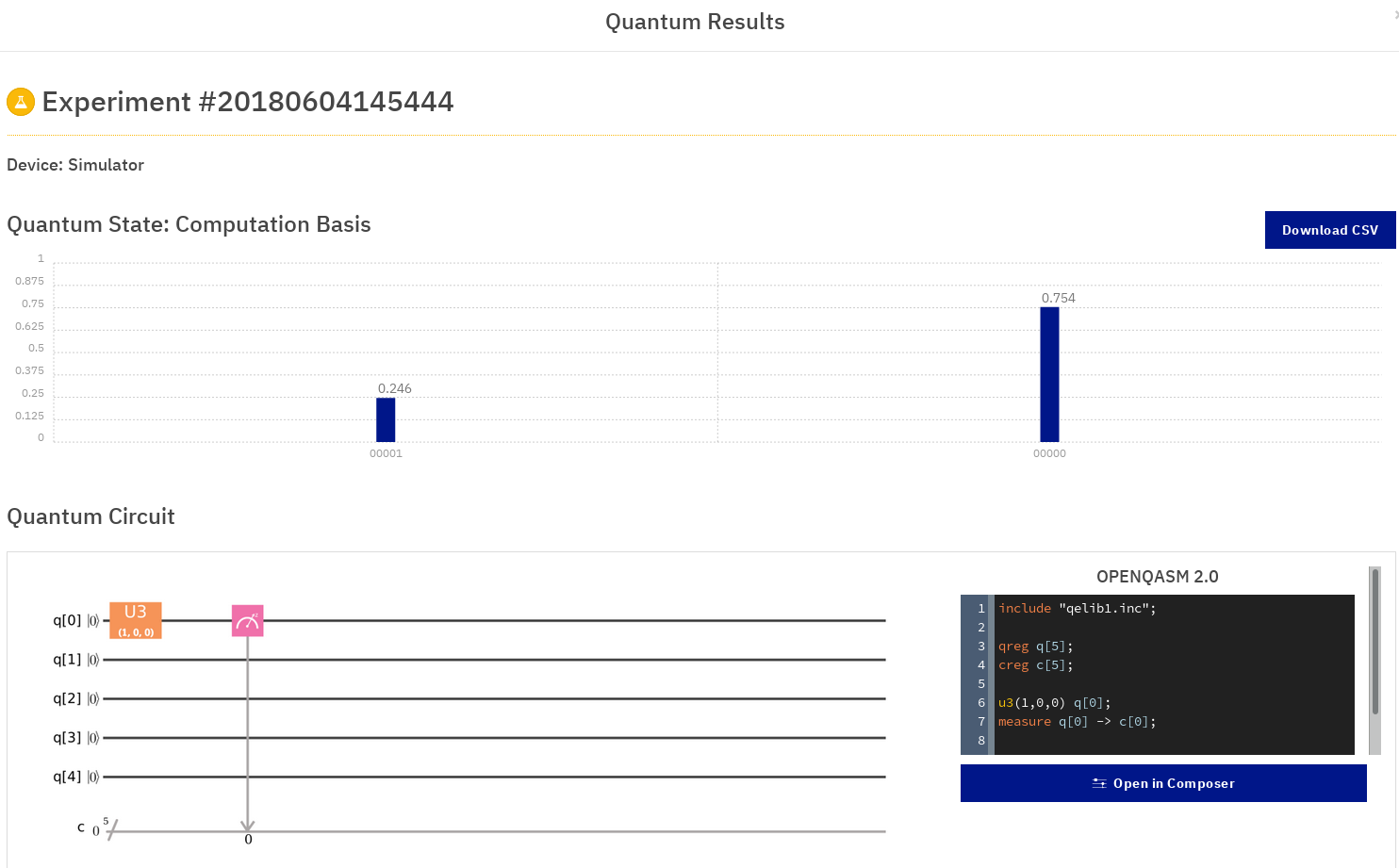
Et on obtient bien un avantage certains pour zéro, puisque qu'avec un angle plus petit sur l'axe Z, notre qubit est plus proche du pôle nord que de l'équateur.
Maintenant que l'on sait comment jouer avec les bases, et qu'on arrive à lire les définitions de quelques portes logiques (qui dans l'interface sont toutes exprimées en tant que rotation), on va pouvoir s'intéresser aux structures de contrôle.
CNOT
La porte Controlled-NOT est assez simple : si un qubit donné est à 1, alors on opère une rotation de Pauli X sur un autre qubit donné. Voici un exemple complet, avec le q[0] qui est choisi aléatoirement grâce à la porte Hadamard, et qui va modifier la valeur de q[1] :
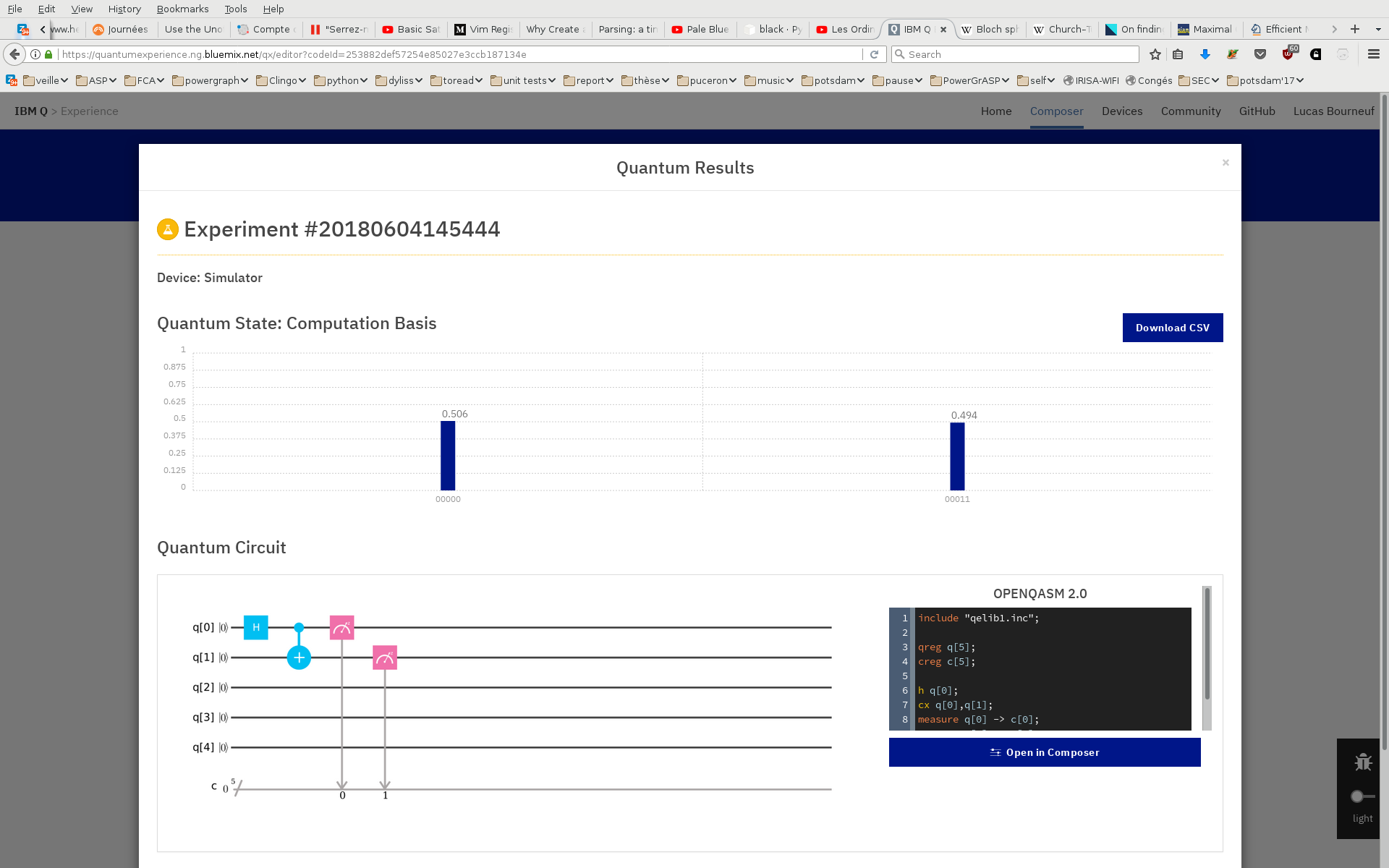
Le résultat est assez évident : dans 50% des cas, q[0] est à 1, donc active la porte CNOT qui opère une rotation de Pauli X sur q[1], qui passe alors à 1. À l'inverse, quand q[0] est à zéro, la porte CNOT laisse q[1] tranquille, il est donc inchangé, c'est-à-dire à 0 dans 100% des cas.
Note sur le quantique II
Si vous essayez de mesurer deux fois la valeur d'un qubit, ou si vous essayez de l'écrire après mesure, l'interface vous renvois une erreur : vous ne pouvez pas jouer avec un qubit après l'avoir lu. C'est une limitation pratique, car j'imagine qu'en théorie, vous pourriez pendant un calcul remettre un qubit à zéro et le réutiliser d'une manière ou d'une autre.
L'autre limite est celle de la lecture : vous ne pouvez pas lire deux fois la valeur. Cela est pratique, pour que l'interface reste simple, il n'y a que deux cas à gérer pour un qubit. En théorie, rien ne m'empêche d'utiliser un qubit, de l'afficher (donc de lui fixer sa valeur), de le réutiliser et de l'afficher encore. Mais là, les devs de chez IBM devraient faire un travail supplémentaire sur l'interface qui ne peut en l'état pas afficher des stats qui prendrais ma tambouille en compte.
Topologie
Quand on veut poser la porte CNOT, on observe certaines limites de placement. Je ne peut pas par exemple mettre la porte CNOT sur q[4] et la faire dépendre de q[1]. Parce que ces deux qubit ne sont pas en relation. En fait, la topologie d'un ordinateur quantique est super importante : elle détermine quel qubit peut-être dépendant que quel autre.
Voici la doc concernant l'ordinateur quantique que j'utilise. En scrollant en bas, on trouve le graphe de cette topologie :

On voit maintenant pourquoi : ils ne sont pas reliés. Et dans ce cas, pourquoi IBM se fait chier avec une topologie ? Eh bien simplement parce que permettre la liaison entre deux qubit vient avec pleins de contraintes techniques, et donc un coût élevé. Ça semble franchement complexe, et il suffit de lire le paragraphe à ce propos pour voir que beaucoup de détails d'implémentation viennent abîmer le magnifique modèle d'un ordinateur quantique à topologie complète.
L'ordinateur quantique D-Wave, qui fonctionne sur un système très différent, est également très limité par cette histoire de topologie : il contient un millier de q-bit, mais chacun ne peut être relié qu'à 3 autres maximum. Ça limite énormément cette histoire !
if
Dans les descriptions, il y a une porte if, mais je ne la trouve pas. Zut. Ce n'est pas la seule porte à manquer d'ailleurs. Probablement ne sont elles disponibles que pour l'ordinateur actuellement en maintenance…
Conclusions
Eh bien, voilà. C'est intéressant, mais avant de pouvoir faire quoi que ce soit avec, il va falloir du temps et de l'expertise. Ça tombe mal, j'ai ni l'un ni l'autre.
L'informatique quantique, c'est une nouvelle méthode de calcul qui arrive. Elle va, si elle remplit ses promesses, révolutionner certains aspects du calcul, et donc de notre société (il y a des chances pour que ce soit la fin de la vie privée, c'est quand même un détail notable).
Quand on s'y intéresse, ça fait diablement penser au tout début de l'informatique, quand des ingénieurs et chercheurs hyper pointus construisaient des machines grosses comme des pièces pour faire quelques malheureux calculs balistiques. Là, c'est pareil, bien que dans un contexte différent : on se rend tous beaucoup mieux compte de ce qui arrive avec ça. On a déjà beaucoup d'outils et de théories sur les langages, les interfaces, et l'informatique en général.
Il a fallut moins d'un siècle pour passer d'une machine de plusieurs tonne calculant des trajectoires à des écosystèmes complets de systèmes inter-connectés qui, juste avec des calculs binaires, permettent à des gens de s'envoyer des vidéos grâce à des stacks de technologies qui s'empilent encore plus vite que des livres recommandés par des amis, évoluant plus vite qu'on ne peut les apprendre et disparaissant dans l'année en laissant place à trois autres équivalents.
Imaginez dans un siècle, avec des interfaces qui permettent d'utiliser votre QPU sans même avoir besoin de comprendre ce qu'est un qubit, comme aujourd'hui on peut faire des jeux vidéos ou un énième framework javascript sans piger un broc au fonctionnement de la logique booléenne («ils font chier avec les maths, je veux juste coder»).
J'imagine que si le quantique est aussi révolutionnaire que l'on aime à le dire, dans un siècle la communauté QJS sera un beau merdier.
Sur une note plus sérieuse : vu les problèmes attaqués par les calculateurs quantiques, l'intérêt d'en avoir un au même titre qu'une GPU semble limité. C'est vrai pour le moment, mais pour combien de temps ? La nécessité d'une carte dédiée aux rendus graphiques ne s'est pas fait sentir immédiatement, et les applications rendues possibles n'ont pas été connues immédiatement. D'où la question : que ferons-nous avec nos QPU ? De meilleurs perfs pour les jeux vidéos ? Des q-crypto-monnaies ? Des oracles sur des problèmes d'optimisations ? Et avec quels langages, au final ? Est-ce que Vulkan proposera un support au calcul quantique ?
Aller plus loin
Si vous avez apprécié ce tour, ce papier est une mine d'or d'informations. L'auteur a fait un module python, Quintuple, qui simule l'ordinateur quantique d'IBM, vous pouvez donc jouer avec le simulateur en étant hors-ligne. Il y a également des algos standards déjà implémentés, prêt à être utilisés, et des forks qui simplifient un peu le code en découplant les nombreux tests de l'implémentation.
Enfin, quelque soit votre langage de prédilection, il y a probablement une, voire plusieurs librairies qui vous permettront de jouer avec des qubits. Voire même des librairies ou des langages pour simuler des ordinateurs quantique !