Comment modéliser le nombre de proies et de prédateurs dans un écosystème en python ?
Question a priori complexe, jusqu'au moment où l'on trouve sur la page wikipédia des équation de Lotka-Volterra les deux équations qui donnent en fonction des populations de proies et de prédateurs leurs variations.
La solution simple consiste en la reproduction des équations qui permettent de calculer à un instant t la population à un instant t+1 :
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
PREY, PRED = 1.9, 1.9
PREY_REPRO_RATE, PREY_DEATH_RATE = 4/3, 2/3
PRED_REPRO_RATE, PRED_DEATH_RATE = 1, 1
TERM_WIDTH = 80
def next_pop(prey:float, pred:float) -> (float, float):
"""Return next amount of preys and predators"""
dprey = prey * 0.1 * (PREY_REPRO_RATE - pred * PREY_DEATH_RATE)
dpred = pred * 0.1 * (prey * PRED_REPRO_RATE - PRED_DEATH_RATE)
return prey + dprey, pred + dpred
def run_model(steps:int=500) -> [(float, float)]:
"""compute population evolution for given steps"""
pop = PREY, PRED
results = [] # or make this yield the pops
for step in range(steps):
pop = next_pop(*pop)
results.append(next_pop(*pop))
return results
def vizualize(pops:[(float, float)]):
"""Build and save graphics of given populations"""
df = pd.DataFrame(pops, columns=('prey', 'pred'))
df.to_csv('out.csv')
plot = df.plot()
plot.grid()
plot.set_xlabel('time')
plot.set_ylabel('population')
plot.set_title('Evolution of populations')
plt.savefig('out.png', dpi=400)
plt.show()
vizualize(run_model())
Grâce à un peu de pandas, on trouve le graphe suivant :
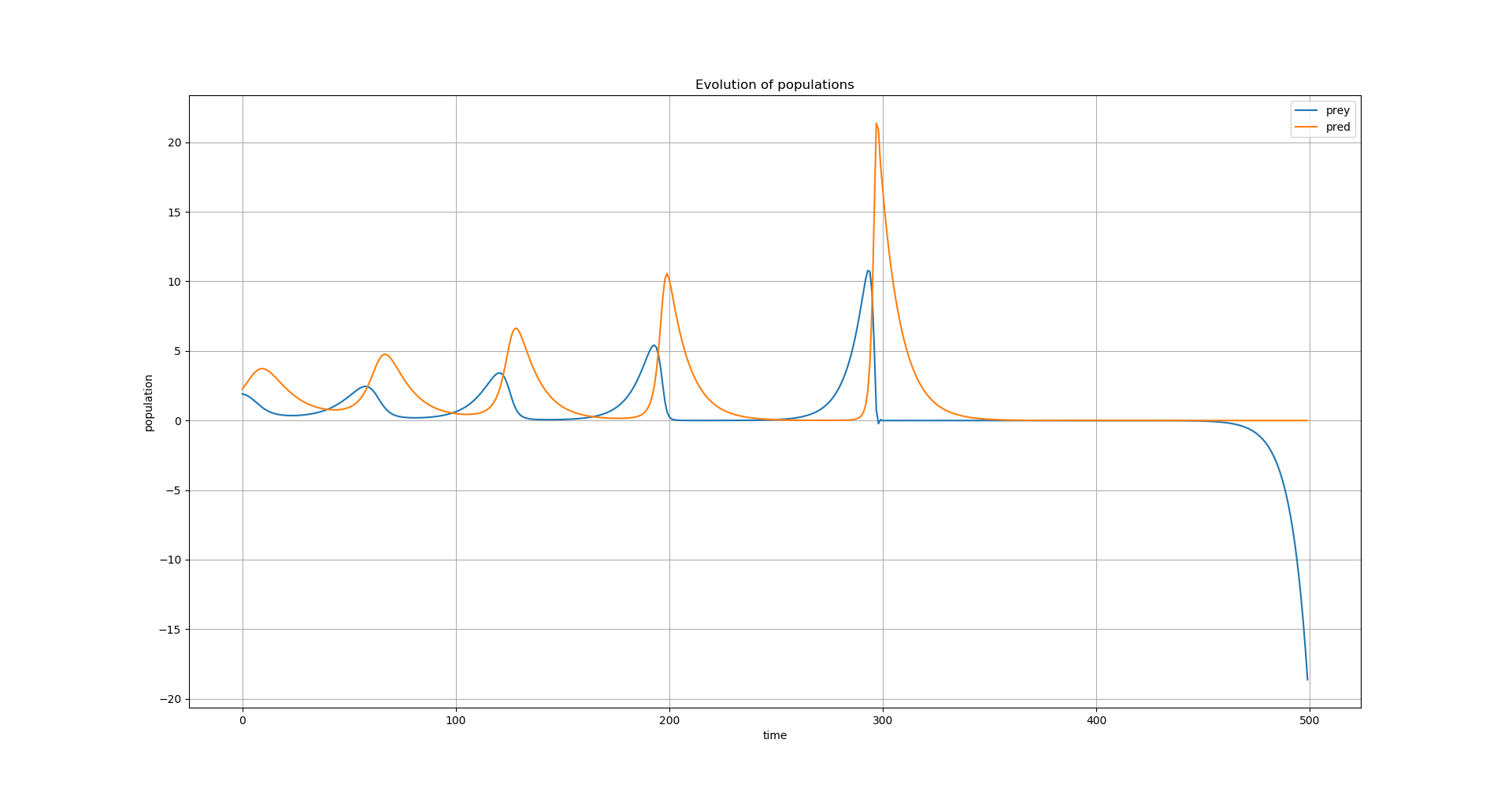
Et là, surprise : on obtient pas la même chose que sur wikipédia. Au lieu des jolies courbes, on a un truc qui part en cacahuète dés 3 oscillations. En jouant un peu sur les paramètres, on arrive parfois à des résultats un poil meilleurs, mais à un moment ou un autre, les oscillations cessent pour laisser la place à une augmentation exponentielle des proies et des prédateurs, ou à la stagnation des populations avec des nombres proches de zéro.
Ça laisse penser à un problème de nombres flottants, hein ?
Eh bien, oui, c'est à peu près ça : les équations différentielles de ce modèle sont non-linéaires, i.e. elles sont chaotiques, ainsi la moindre erreur d'arrondis dû à la finitude de nos ordinateurs pollue complètement le système.
C'est ce que l'on observe, et ce dont on ne veut pas. La solution ? Ici, on a utilisé la méthode d'Euler pour la résolution d'équation différentielles, c'est-à-dire que pour connaître l'état du système à l'instant t+1, on applique la formule à l'intant t. C'est simple, mais trop simple. En général, cette méthode n'est pas utilisée, car ses résultats, même dans le cas d'équations linéaires, sont pas géniaux, justement à cause de la finitude de nos ordinateurs.
D'où l'existence de modèle de résolution un poil plus complexe, mais beaucoup plus puissants, notamment la généralisation de la méthode d'Euler, Runge-Kutta. Nous allons donc profiter de cette nouvelle méthode, et surtout de l'implémentation en python proposée par scipy pour gérer la crise:
import numpy as np
import pandas as pd
from scipy import integrate # il n'y a pas Runge-Kutta dans le nom, mais c'est bien elle
import matplotlib.pyplot as plt
# Parameters
PREY_REPRO_RATE, PREY_DEATH_RATE = 1.5, 0.75
PRED_REPRO_RATE, PRED_DEATH_RATE = 1., 0.1
PREY, PRED = 10, 5
def next_pop(pops, t):
"""Return populations growth"""
prey, pred = pops
return np.array([prey * (PREY_REPRO_RATE - PREY_DEATH_RATE*pred),
pred * (PRED_DEATH_RATE*prey - PRED_REPRO_RATE)])
def vizualize(pops:[(float, float)]):
"""Build and save graphics of given populations"""
df = pd.DataFrame(pops, columns=('prey', 'pred'))
df.to_csv('out.csv')
plot = df.plot()
plot.grid()
plot.set_xlabel('time')
plot.set_ylabel('population')
plot.set_title('Evolution of populations')
plt.savefig('out.png', dpi=400)
plt.show()
populations = integrate.odeint(next_pop, [PREY, PRED], np.arange(0, 30, 0.1))
vizualize(populations)
Et là, magie, on obtient:
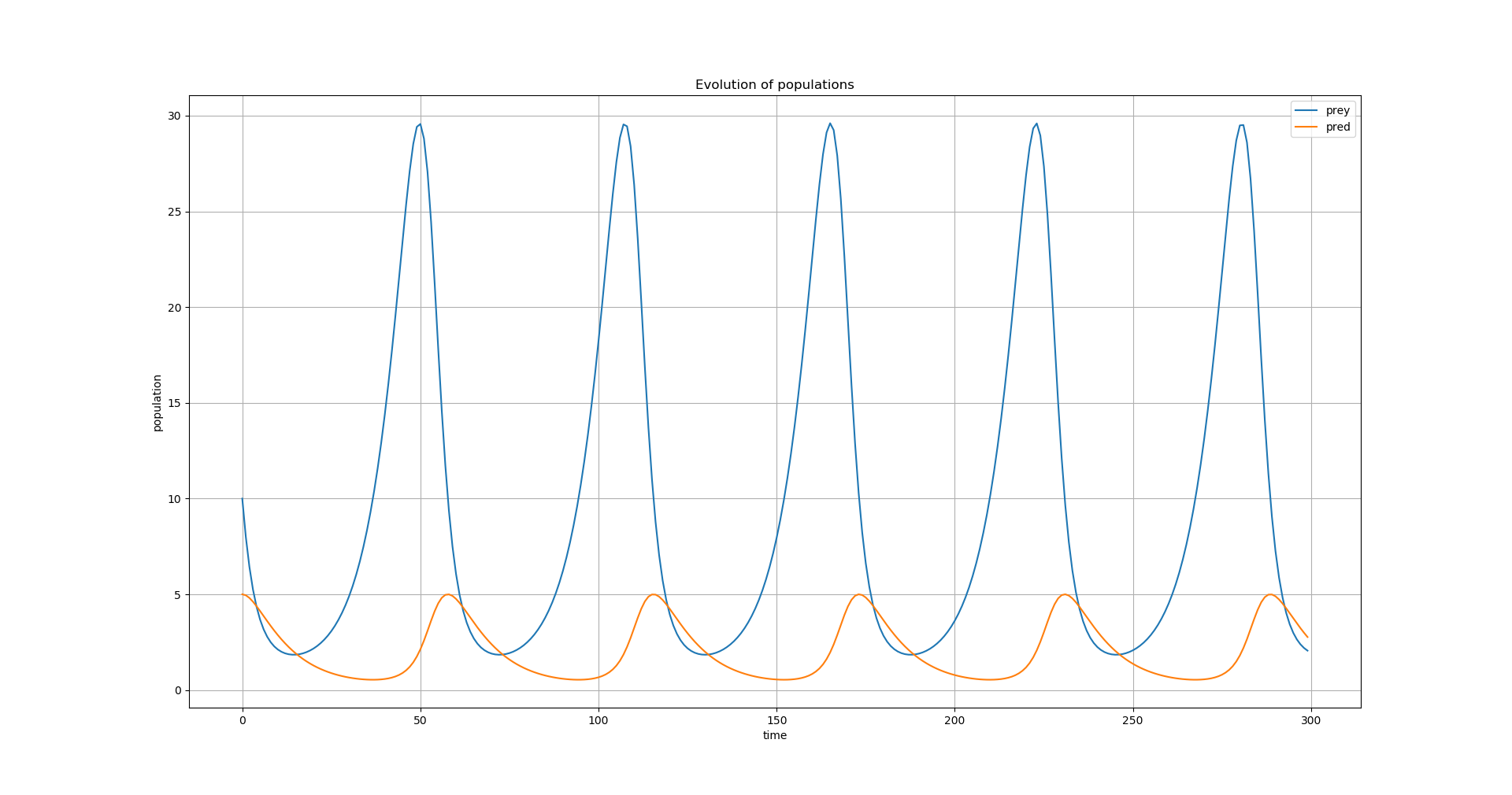
La différence, c'est principalement l'appel à scipy.integrate.odeint qui prend en argument la fonction de calcul de l'étape suivante, les populations initiales,
et l'intervalle de temps sur lequel travailler. C'est-à-dire le minimum syndical pour calculer ce que l'on veut afficher : les quantités de proies et de prédateurs à chaque étape.
Notez que la fonction vizualize n'a pas changée d'un char, puisque l'entrée n'a pas changée non plus, et next_pop est restée globalement la même
mis à part l'usage de numpy et l'argument t qui donne le step (permettant d'avoir des paramètres dépendant du temps… Ça donne des idées… hivernales).
C'est donc bien run_model qui est intégralement remplacée par scipy.integrate, et qui se charge, seule, de boucler sur des appels successifs de next_pop,
et fait ses petits calculs pour obtenir des valeurs de population plus réalistes que ceux que l'on a eu plus tôt avec la méthode d'Euler.
Les petits calculs en question, ce sont principalement de multiples appels à next_pop avec des valeurs autour de celle attendue pour comprendre
comment se comporte réellement la fonction, et donc prédire avec une meilleure précision l'évolution réelle des populations.
Pour voir un peu ce comportement, il suffit d'ajouter un print dans la fonction next_pop, montrant les arguments utilisé pour le calcul d'un seul pas :
import numpy as np
import pandas as pd
from scipy import integrate # il n'y a pas Runge-Kutta dans le nom, mais c'est bien elle
import matplotlib.pyplot as plt
# Parameters
PREY_REPRO_RATE, PREY_DEATH_RATE = 1.5, 0.75
PRED_REPRO_RATE, PRED_DEATH_RATE = 1., 0.1
PREY, PRED = 10, 5
def next_pop(pops, t):
"""Return populations growth"""
prey, pred = pops
print('CALL:', prey, pred)
return np.array([ prey * (PREY_REPRO_RATE - PREY_DEATH_RATE*pred),
pred * (PRED_DEATH_RATE*prey - PRED_REPRO_RATE)])
# un seul pas est calculé
populations = integrate.odeint(next_pop, [PREY, PRED], np.arange(0, 0.2, 0.1))
Et là, on obtient la liste des 31 appels réalisés par l'implémentation de Runge-Kutta :
CALL: 10.0 5.0
CALL: 9.999730912906742 5.0
CALL: 9.999730920147528 4.999999998390936
CALL: 9.999461840294956 4.999999996781959
CALL: 9.999461847535692 4.999999995172939
CALL: 9.94360342651676 4.999964459862722
CALL: 9.943603310697434 4.999964557771127
CALL: 9.888058340902473 4.99985958511471
CALL: 9.888058100892646 4.999859781746022
CALL: 9.832825975292891 4.9996858633388115
CALL: 9.832825722322942 4.99968606108886
CALL: 9.695979811385243 4.998951105232745
CALL: 9.695978983283519 4.998951636609206
CALL: 9.561078660548603 4.997794812170416
CALL: 9.56107892134775 4.997794327484126
CALL: 9.428116308219263 4.996220344102796
CALL: 9.428115928006864 4.996220373884703
CALL: 9.297079677432846 4.994236151039088
CALL: 9.297079316463563 4.9942361772575055
CALL: 9.055355412989126 4.989405075150046
CALL: 9.055354077242372 4.989405160359211
CALL: 8.820342103568848 4.983184252891582
CALL: 8.820343266625454 4.983184132413643
CALL: 8.591952233519647 4.975617397872972
CALL: 8.591953332004437 4.975617282835056
CALL: 8.370082718245143 4.966749130817226
CALL: 8.370083090789096 4.966749072646591
CALL: 8.154623968890911 4.956624182943434
CALL: 8.154624324462075 4.956624128056839
CALL: 7.808215969644887 4.936999679158772
CALL: 7.808217446408007 4.936999456289741
Notons également que si le pas de temps est agrandi (np.arange(0, 2, 1)), beaucoup plus d'appels sont réalisés, pour compenser la perte de résolution.
Sinon, l'autre solution pour simuler un système proie-prédateur, c'est encore l'automate cellulaire qui génère des courbes en temps réel. Pas de maths, pas de scipy, juste des boucles, des if, du random et un rendu graphique.