La fonction Rollin est décrite par François Rollin, dans l'un des contes de Noël et du Nouvel An du Professeur Rollin.

Cette fonction permet au professeur Rollin de montrer la spécificité de l'année 2005, car la fonction associe 3 à cette année là. 3, en Champagne.

Description de la fonction pour 2005 :

• je multiplie 2005 par -52, date de la bataille d'Alésia
• j'y ajoute 5 fois la population de Bethléem, soit 5 × 21947, ce qui donne 5475
• je divise ce chiffre par le numéro atomique du Tantale, 73
• j'obtiens 75 («tout rond, c'est déjà pas banal»)
• j'additionne le 7 et le 5, donc 12
• 1 + 2 = 3… en Champagne !

D'après le professeur, le même procédé appliqué à l'année 1922 donne 5.

Une première interprétation pour la fonction décrite est la suivante :

def somme_chiffre(nb:int) -> int:
    return sum(map(int, str(nb)))

def rollin(annee:int) -> int:
    nb = ((-52 * annee) + (5 * 21947)) / 73
    while len(str(nb)) > 1:
        nb = somme_chiffre(nb)
    return nb

assert rollin(2005) == 3
assert rollin(1922) == 5

Ah, tout fonctionne pour le premier cas, 2005. Néanmoins, une erreur est levée pour 1922, suggérant que notre fonction n'est pas celle du professeur. Pas d'inquiétude cependant, nous connaissons le résultat attendu (5), et plusieurs manières pour améliorer notre interprétation.

Décisions sur décimaux

L'erreur est question est dû à un problème concernant les nombres décimaux : ((-52 * 1922) + (5 * 21947)) / 73 n'est pas un nombre entier : 134.12328767123287. Notre fonction ne fonctionne plus, et pire, le professeur ne nous a pas indiqué comment la fonction devait se comporter lorsque la division renvoie un nombre décimal.

Une première zone d'ombre sur la définition de la fonction plane donc sur la gestion des nombres décimaux. Voici trois moyens pour gérer la crise.

Troncature

Définissons la fonction somme_chiffre légèrement différemment, par troncature de la partie décimale :

def somme_chiffre(nb:int) -> int:
    return sum(map(int, str(int(nb))))

Maintenant, dans le cas de l'année 1922, nous obtenons 8 : en effet, la partie décimale étant ignorée, nous sommons les chiffres du nombre 134, soit 1 + 3 + 4 = 8. Ça fonctionne, mais ce n'est pas en accord avec ce qu'indique le professeur. Raté.

Retrait du point

Définissons la fonction somme_chiffre de telle manière que le point dans les nombres décimaux soit ignoré :

def somme_chiffre(nb:int) -> int:
    return sum(map(int, str(nb).replace('.', '')))

Dans un tel cas, nous arrivons à 1+3+4+1+2+3+2+8+7+6+7+1+2+3+2+8+7=67, soit 6+7=13, donc 4. Ce n'est pas, bien que l'on s'en rapproche comme le requin d'un surfeur, encore la solution indiquée par le professeur.

Arrondis

Considérons que le professeur Rollin ne s'intéresse pas à des mondanités telles que l'exactitude des nombres flottants. Après tout, Turing ne s'est pas intéressé à la complexité des machines du même nom, et deux décimales de pi sont suffisantes pour envoyer des cosmonautes sur la lune.

Question : quel arrondis permet à la fonction Rollin de trouver 5 pour 1922 ? Trouvons la réponse par brute-force :

def somme_chiffre(nb:int) -> int:
    return sum(map(int, str(nb).replace('.', '')))

def rollin(annee, arrondis:int=0) -> int:
    nb = round(((-52 * annee) + (5 * 21947)) / 73, arrondis)
    while len(str(nb)) > 1:
        nb = somme_chiffre(nb)
    return nb

for arrondis in range(20):
    assert rollin(2005) == 3  # on vérifie qu'on est toujours ok
    if rollin(1922, arrondis) == 5:
        print(arrondis)

Et nous obtenons trois valeurs : 3, 6 et 11. Nous avons donc trois candidats. En appliquant pratiquement des théorèmes, tels que le rasoir d'Ockham ou le théorème du choix, nous pourrions dire que nous avons le choix de choisir parmi le plus économe, c'est-à-dire l'arrondis le plus tronquant. Cependant, ce serait oublier que 2005 est l'année la plus spécifique, parmis toutes les années contemporaines du professeur Rollin au moment de la définition de la fonction éponyme, c'est-à-dire de 1953 à 2005. Par conséquent, afin de discriminer la meilleure solution, regardons le nombre d'années spécifiques en fonction de l'arrondis choisi :

for arrondis in (3, 6, 11):
    print(str(arrondis).rjust(2), end=': ')
    for annee in range(1953, 2006):
        if rollin(annee, arrondis) == 5:
            print(annee, end='\t')
    print()

Et nous trouvons :

 3: 1956    1963    1970    1983    1990    1997
 6: 1961    1964    1975    1986    1989    2000
11: 1956    1963    1970    1983    1990    1997

Ah. C'est embêtant, car, voyez-vous, les trois arrondis possibles proposent tout trois 6 années spécifiques. C'est fort embêtant. Notez que commencer non pas en 1953, mais en 1922, ne change rien au problème. Il faut remonter plus loin, par exemple l'année où le russe devient la langue officielle de l’administration finlandaise, ou l'année où Henri V est couronné empereur par le pape, aussi appelée par abus de langage, l'année de l'invasion des uns (sans h), afin de voir une asymétrie naître.

Nous noterons d'ailleurs dans de tels cas les intéressantes similitudes entre 3 et 11, laissant 6 sur le carreau de la différence. Après réflexions et discussions avec un ami pas plus mathématicien que moi (mais néanmoins plus grand, peut-être cela n'a-t-il rien à voir), il apparaît que cette propriété n'est pas un hasard, car dans la première partie de la fonction de Rollin se trouve la division par 73, un nombre premier. Plus précisément, il semblerait que toute division par le numéro atomique du tentale donne un nombre décimal de période 8, ainsi les arrondis à 3 et à 11 tronquent-ils la valeur au même index de la période, donc à la même valeur (sauf dans des cas particuliers dûs à de malheureux arrondis), se traduisant, d'une manière qui m'échappe encore, en une équivalence lors de la somme en seconde partie de la fonction.

Rien d'exploitable, donc.

Du multiplicateur de la population de Bethléem

Notons un détail qui ressemble à une coïncidence : nous multiplions la population de Bethléem par le dernier chiffre de l'année, 5. Et si il ne s'agissait pas d'un hasard ?

Peut-être que la fonction Rollin utilise le dernier chiffre de l'année pour multiplier la population de Bethléem ? Essayons !

def somme_chiffre(nb:int) -> int:
    return sum(map(int, str(nb).replace('-', '').replace('.', '')))

def rollin(annee) -> int:
    nb = ((-52 * annee) + (int(str(annee)[-1]) * 21947))
    while len(str(nb)) > 1:
        nb = somme_chiffre(nb)
    return nb

assert rollin(2005) == 3
print(rollin(1922))  #  -> 3

Raté ! La fonction nous renvois 3. C'est fort embêtant. Mais peut-être avons nous raté le plus important : zéro + zéro + cinq est égal à cinq ! Ainsi, voilà une nouvelle proposition : le multiplicateur de la population de Bethléem est la somme des chiffres de l'année, à l'exception du premier. Pour l'année 1922, nous devons donc multiplier la population de Bethléem non pas par 5, ni par 2, mais bien par 9+2+2=13 !

def somme_chiffre(nb:int or str) -> int:
    return sum(map(int, str(nb).replace('-', '').replace('.', '')))

def rollin(annee, arrondis:int=0) -> int:
    nb = ((-52 * annee) + (somme_chiffre(str(annee)[1:]) * 21947)) / 73
    while len(str(nb)) > 1:
        nb = somme_chiffre(nb)
    return nb

assert rollin(2005) == 3
print(rollin(1922))  #  -> 5

Oui ! Nous avons trouvé ! Notre interprétation de la fonction de Rollin fonctionne ! Nous obtenons bien 5 !

Autres pistes

De la population de Bethléem

Le professeur Rollin est clair : la population de Bethléem est celle recensée en 2002, c'est-à-dire 3 ans avant l'année considérée. 1 ans avant, c'est les impôts, 2 ans avant on sait pas trop, 3 ans avant, c'est la population de Bethléem.

Deux cas existent :

• soit le choix de l'année 2002 est absolu, c'est-à-dire qu'il ne dépend pas de l'année. Dans ce cas, la fonction Rollin n'est calculable que depuis 2002, année de la liquidation de la compagnie aérienne Swissair. Suisse. Ce pourrait ne pas être un hasard.
• soit le choix de l'année 2002 est relatif à l'année considérée, peut-être simplement par une décrémentation de 3, indiquant que la population de Bethléem de 1919 doit être considérée pour calculer la fonction de Rollin.

Cette seconde solution est embêtante pour deux raisons : - Bethléem ayant été fondée il y a très longtemps, et le recensement n'étant que très récent, cela rend la fonction de Rollin incalculable pour la majorité de son temps d'existance. Le rasoir d'Ockham nous indiquant que la solution la plus simple étant toujours la meilleure, nous devons nous abstenir de rajouter des incertitudes sur une fonction que l'on peut expliquer plus simplement. - au risque de me répéter, la population de Bethléem devient un second argument pour la fonction. C'est chiant. Une belle fonction en mathématique, elle n'a qu'un seul paramètre, ou alors elle est enseignée dans les écoles d'ingénieurs.

Donc, bon, bof. Mais à garder dans un coin de la tête pour le jour où on devra oublier des choses.

De l'interprétation de l'addition des chiffres

Dans sa démonstration, le professeur ne s'intéressant qu'à un cas particulier, il nous est impossible de déterminer si l'addition des chiffres 7 et 5 qui font 12 et 1 et 2 qui font 3 doit se faire jusqu'à épuisement de chiffres, ou uniquement deux fois.

La première solution à été retrouvée ici, mais en réalité une recherche approfondie serait bienvenue, montrant les effets que pourraient avoir un nombre donné d'addition des chiffres. Peut-être deux est-il suffisant, peut-être en faut-il autant que la population à Troy. La question est ouverte.

La fonction Rollin

Voici donc, au terme de nos recherches, notre interprétation la plus solide de la fonction Rollin :

def somme_chiffre(nb:int) -> int:
    return sum(map(int, str(nb).replace('-', '').replace('.', '')))

def rollin(annee) -> int:
    nb = ((-52 * annee) + (sum(map(int, str(annee)[1:])) * 21947)) / 73
    while len(str(nb)) > 1:
        nb = somme_chiffre(nb)
    return nb

assert rollin(2005) == 3
assert rollin(1922) == 5

Nous pouvons maintenant nous poser la question de cette fonction dans sa représentation graphique !

Les codes générant les visualisations qui suivent sont disponibles sur mon dépôt. Notez également que certaines sont générées avec pyqtgraph. C'est une (très agréable) découverte pour moi.

Voici un code plus simple qui reproduit à peu près les résultats, en utilisant la trinité matplotlib/pandas/seaborn :

import seaborn as sbn
import pandas as pd
import matplotlib.pyplot as plt

# Une palette commune sympa.
sbn.set()
sbn.set_palette('husl', 10)

# Construction des données
BOUNDS = 1922, 2005
ANNEES = range(BOUNDS[0], BOUNDS[1]+1)
ROLLIN = tuple(rollin(annee) for annee in ANNEES)
def evolution(nbs:[int], start:int) -> [int]:
    prev = start
    for nb in nbs:
        nb, prev = nb - prev, nb
        yield nb
EVOLUTION = tuple(evolution(ROLLIN, rollin(BOUNDS[0] - 1)))
GREEN = (119,172,48)
RED = (200,12,48)

# Association nombre de Rollin -> années
ANNEE_PAR_NB = {}  # nombre de rollin -> {années}
for annee, nb_rollin in zip(ANNEES, ROLLIN):
    ANNEE_PAR_NB.setdefault(nb_rollin, []).append(annee)

# Simple plot de la trace de la fonction
nb_par_annee = pd.DataFrame({
    'année': ANNEES,
    'nombre de Rollin': list(rollin(annee) for annee in ANNEES)
}).set_index('année')
ax = nb_par_annee.plot(legend=False)
ax.set_title("Nombre de Rollin en fonction de l'année ({}-{})".format(*BOUNDS))
ax.set_xlabel("Année")
ax.set_ylabel("Nombre de Rollin")
plt.show()

# Plot de l'évolution du nombre de Rollin
nb_par_annee = pd.DataFrame({
    'année': ANNEES,
    'nombre de Rollin': EVOLUTION,
}).set_index('année')
ax = nb_par_annee.plot(legend=False)
ax.set_title("Évolution du nombre de Rollin d'une année à l'autre ({}-{})".format(*BOUNDS))
ax.set_xlabel("Année")
ax.set_ylabel("Nombre de Rollin")
plt.show()

# Nombre d'années pour chaque nombre de Rollin
nb_annee_par_nb = {"nombre d'années": [], 'nombre de Rollin': []}
for nb, annees in ANNEE_PAR_NB.items():
    nb_annee_par_nb["nombre d'années"].append(len(annees))
    nb_annee_par_nb["nombre de Rollin"].append(nb)
nb_annee_par_nb = pd.DataFrame(nb_annee_par_nb).set_index('nombre de Rollin').sort_index()
ax = nb_annee_par_nb.plot.bar(y="nombre d'années", rot=0, legend=False)
ax.set_title("Dénombrement des années {}-{} selon leur nombre de Rollin".format(*BOUNDS))
ax.set_xlabel("Nombre de Rollin")
ax.set_ylabel("Nombre d'années")
for patch in ax.patches:  # show the total count above each bar
    b = patch.get_bbox()
    ax.annotate(str(int(b.y1)).rjust(3), (patch.get_x() - 0.04, b.y1 * 1.01))  # MAGIC
plt.show()

# Boxplot, pour avoir une idée de la distribution des années
df_annee_par_nb = pd.DataFrame(
    {k: pd.Series(v) for k, v in ANNEE_PAR_NB.items()},
    columns=sorted(tuple(ANNEE_PAR_NB.keys())),
)
ax = df_annee_par_nb.boxplot(rot=0)
ax.set_title("Distribution des années {}-{} selon leur nombre de Rollin".format(*BOUNDS))
ax.set_xlabel("Nombre de Rollin")
ax.set_ylabel("Distribution des années")
plt.show()

Représentation scolaire

Comme à l'école, montrons la courbe de la fonction selon la valeur en abscisse. Intéressons-nous d'abord aux années 1922 à 2005 :

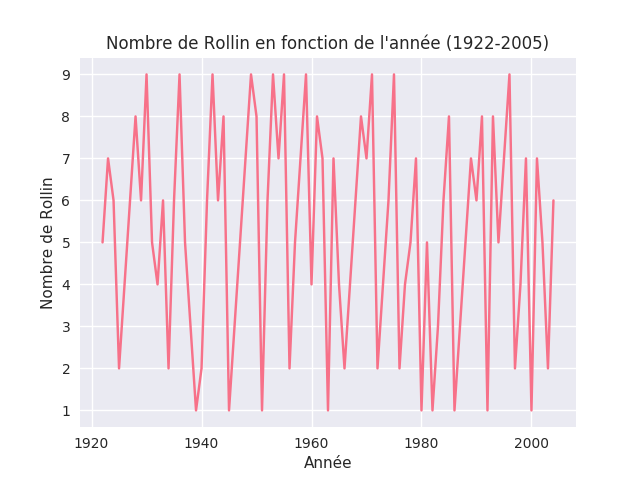
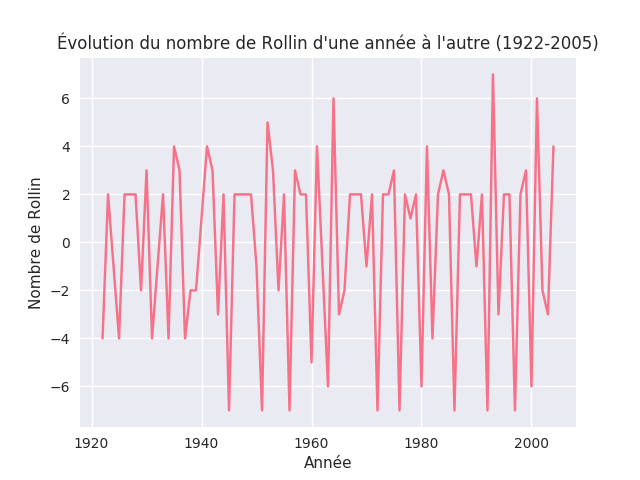
La courbe ne montre à priori aucune régularité évidente, et ceci est appuyé par la visualisation de l'évolution du nombre de Rollin :

Maintenant, regardons pour les années de 1 à 2005 :

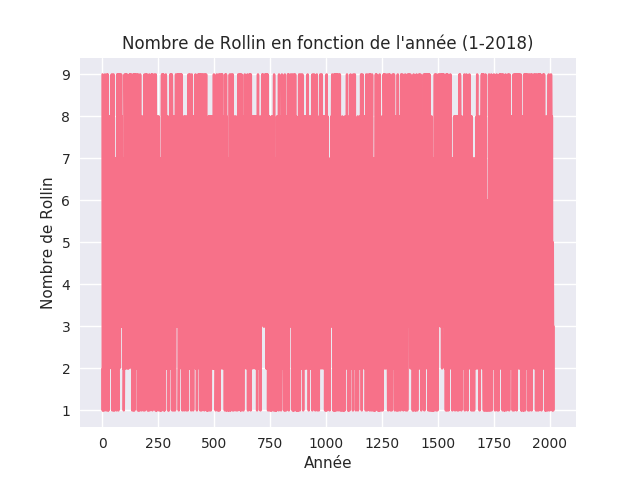
C'est moche ! Notons que la visualisation laisse entendre que les extrêmes sont sous-représentés. Comme nous le verrons plus tard, une telle sous-représentation n'est pas visible. Il s'agit en réalité d'un artefact de visualisation, probablement dû à un effet graphique (qui a certainement un nom très connu parmi ceux qui le connaissent déjà), où la ligne symbolisant le nombre 5 est polluée par toutes les transitions d'un nombre supérieur à 5 vers un autre inférieur à 5, ou inversement, soit 5 × 5 × 2 = 50 transitions possibles. Dans le même temps, il n'existe aucun moyen de polluer de la sorte la ligne des nombres 1 et 9 (qui sont aux extrémités), puisque la courbe ne croise jamais ces lignes, et les seules transitions qui polluent la ligne 8 sont celles qui impliquent un 9, c'est-à-dire 1 × 7 × 2 = 14, ce qui explique également l'apparente faible densité pour les lignes 2 et 8, et par récurrence celle des lignes 3 et 7 (2 × 6 × 2 = 24).

Nombre d'années par nombre de Rollin

Une représentation plus intéressante serait de montrer le nombre d'années concernées par chaque nombre de Rollin. En d'autres terme, combien y a-t-il d'années à 1 ? À 2 ? À 3 ? Regardons d'abord le comptage pour les années 1 à 2018 :

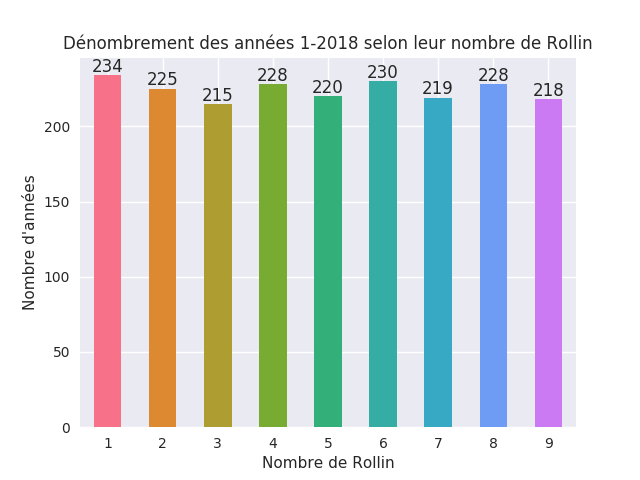
Bon, sur de larges périodes, on observe une distribution uniforme. Cela étant dit, notons la place particulière des années de nombre de Rollin 3, qui sont les moins représentées. Là où c'est carrément questionnable, c'est sur les périodes récentes, où les résultats sont encore plus remarquables :

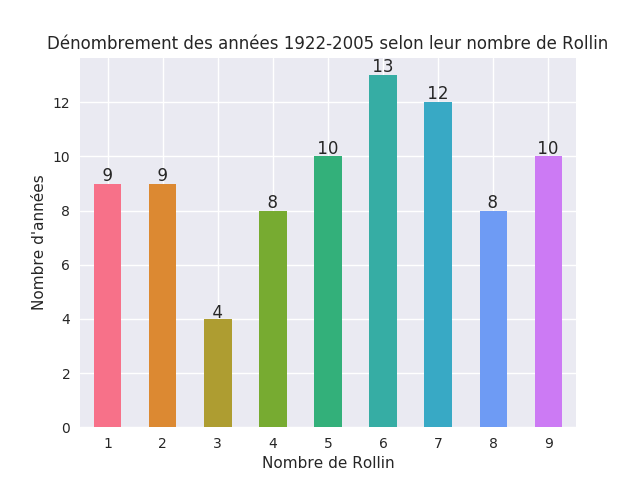
On retrouve les même résultats en lançant le programme pour les années -8000 à 8000. On observe donc que ces dernière années particulièrement, mais également de manière générale, le nombre d'année ayant un nombre de Rollin de 3 est sous-représenté. Intéressant.

Dernière remarque : la fonction de Rollin ne suit pas, dans les cas étudiés, la loi de Benford. Si tel était le cas, nous verrions une sur-représentation des années à petit nombre de Rollin, donc beaucoup de 1 et 2, mais peu de 8 ou 9. Objectivement, c'est emmerdant, car la fonction de Rollin n'est pas utilisable pour la falsification de compte.

Boxplot de la distribution des données

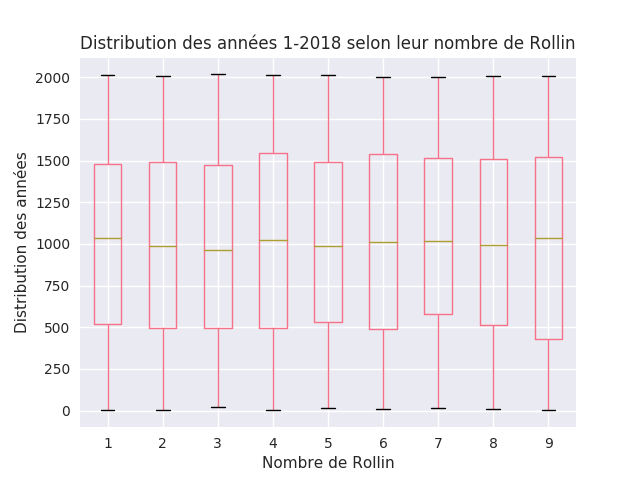
Comment sont réparties les années ? De ce point de vue, sur plusieurs dizaines de générations, la fonction de Rollin est à l'image de l'humanité vue en gros : monotone (au sens où on se fait chier, pas au sens mathématique), c'est-à-dire des distributions avec des moyennes, médiane et écarts à la moyenne très proches, voire identiques.

D'aucun dit que l'histoire se répète, au point de devenir lassante ? La fonction Rollin nous le montre avec virtuosité ! Mais que se passe-t-il si on zoom sur une ou deux générations ?

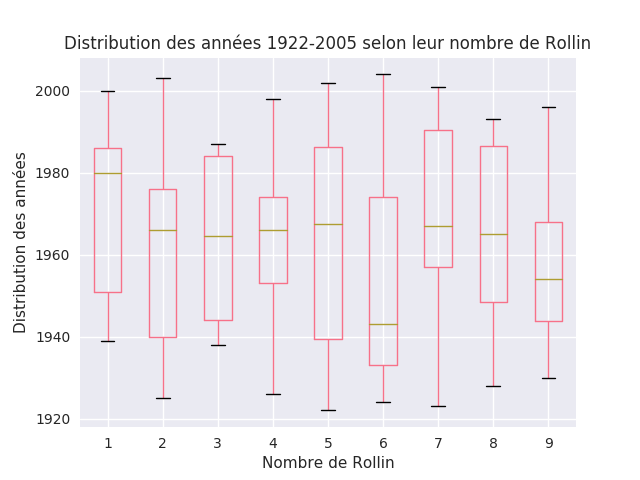
C'est tout de suite plus intéressant ! Notez encore le statut particulier des chem… des années avec un nombre de Rollin de 3 !

Ce comportement traduit une fonction à taille humaine : intéressez-vous à l'humanité entière, elle ne peut pas être appréhendée ; mais regardez-la à l'échelle d'une vie humaine, elle révèle des richesses insoupçonnées.

Autres propriétés de la fonction Rollin

Nullité unique

La seule valeur pour laquelle la fonction Rollin ne donne pas un nombre de Rollin entre 1 et 9 inclus, c'est l'année zéro, où elle donne… zéro. Ce comportement peut sous-entendre le statut particulier d'une année pivot. Ou alors juste que le calcul n'est pas prévu pour remonter à des temps où de toute façon personne ne connaissait la fonction de Rollin, donc pourquoi se faire chier à gérer leurs années à la con, à ces ignorants.

Inversion sur les années négatives

Un intéressant phénomène se produit lorsqu'on étudie les années -2000 à -1 : les années au nombre de Rollin de 3 sont sur-représentées, et non plus sous-représentées ! Une hypothèse intéressante est celle du domaine limité de définition de la fonction Rollin : si elle n'est valide que depuis l'existence du compté de Champagne (rattaché à la couronne sous ce nom durant l'année 1284), cela résouds le problème de nullité à zéro, ainsi que l'interprétation des résultats dans les années négatives. En effet, dans le cas où l'hypothèse serait vérifiée, toute interprétation de la fonction pour une année antérieure à la création de la Champagne relèverait du non-sens, puisque la fonction n'est pas définie pour l'année considérée.

La fonction de Rollin devrait alors renvoyer une erreur pour tout appel invalide, comme cela est fait pour le calcul de l'arcsinus de pi. Voici les lignes à ajouter dans notre implémentation de la fonction Rollin, avant tout traitement :

    if annee < 1284:
        raise ValueError("math domain error")

De la particularité des années Rollin

Les années Rollin, donc, sont des années dont le nombre de Rollin, donné par la fonction de Rollin lorsqu'elle prend en entrée l'année considérée, est 3. Ces années sont, des mots du professeur, Rollin également, spécifiques.

Le professeur n'ayant pas été très volubile à ce sujet, certainement dans un but pédagogique, nous nous devons d'étudier cela en détail. Afin d'étudier de manière complète et neutre les spécificités des années Rollin, nous pourrions utiliser comme corpus les pages wikipédia qui listent, pour chaque année, les grand achèvements de l'humanité et de son environnement.

Le corpus d'apprentissage sera donc récupéré selon la méthode RACHE, c'est-à-dire avec un parsing des pages web concernées de l'apannage d'un vomi de fin de soirée : dégueux mais simple. Une fois les phrases récupérées, elles seront apprise par un modèle de Markov d'ordre 2 sur les mots, car cela donne de bon résultats sur le travail de Victor Hugo. En utilisant en mode génératif ce modèle de Markov ainsi généré, nous obtiendrons des phrases que d'aucun pensera d'aléatoire, et que les poseurs de question impertinants qualifierons de «non sens infondé».

Néanmoins, le professeur Rollin n'ayant jamais tord, il est évident que les années Rollin portent une caractéristique. Si cette caractéristique a trait aux achèvements de l'humanité et de son environnement, cela veut dire que cette caractéristique se trouvera dans le modèle de Markov, et donc que ce même modèle génèrera des prédiction pour les prochaines années Rollin. Sinon, on a démontré que les années Rollin n'ont pas en spécificité d'être liées à des évènements mondains.

Quoiqu'il en soit, nous pouvons créer un générateur à choses qui seront peut-être vraies plus tard. Les codes finaux sont dispos sur le dépôt.

Nous obtenons ainsi quelques vues sur notre futur, telles que :

• Eugene Cernan, astronaute américain, dernier homme ayant marché sur la propriété intellectuelle touchant au commerce.
• 13e Festival international du film de Berlin au Niger.
• La police de Montréal subit de violents orages qui occasionnent des inondations dans le cadre de la ville de deux.
• Une constitution est publiée par le gouvernent de Tchang Kaï-chek, transporte la capitale du pays, cause la mort d'un Texan en 2001, le jury a condamné Merck à verser 229 millions de morts si le virus est en visite dans le sud-ouest de l'Allemagne. Le train était affrété par une foule d'admirateurs en délire.
• Soulèvement intégraliste au Brésil. Les intégralistes (extrême droite) tentent de prendre Valence, mais sont repoussés par les Japonais.
• Madonna donne son premier procès à Klaus Barbie, ancien chef de l’État dans la psychiatrie hospitalière, ainsi que sur le chromosome 10q22, code un nouveau report des élections prévues le 30 avril. Robert Bourassa veut y faire reconnaître ses cinq demandes dites minimales: la reconnaissance du romanche comme langue nationale.
• Le groupe chinois Johnson Electric reprend le lancement du premier journal franco-yukonnais L'Aurore boréale.
• Le deuxième congrès africain du pétrole a réuni des troupes italiennes en Irak.
• Le groupe sud-africain Ladysmith Black Mambazo a été réélu avec 79,18% des suffrages selon les chiffres publiés par la Turquie.
• Le médicament n’est pas un produit comme les autres partis.
• Michael Skibbe devient le 19e pays membre de la grippe aviaire en raison de l’extension rapide de la IVe République dans le secteur du textile
• Le président de l'UCECAO a déclaré qu’il se maintiendra en tant que 265e pape de l'histoire.
• La drépanocytose est une maladie mystérieuse qui a battu le record du monde de handball masculin.

Et enfin, mention spéciale à celui-ci, qui raconte une histoire palpitante :

La population française se monte à 40,5 millions de dollars US, actuellement bloqués sur un marché évalué à 38 millions d'euros et la communauté scientifique internationale ne peut rester insensible au défi visant à enrayer ce qui constitue un élément fondamental de la norme internationale ISO/CEI 27001, concernant les conditions de travail du Sénégal qui a connu une flambée, avec 3400 cas dont 54 décès recensés à travers une porte de cabine du motel Le Châtillon, tuant le poseur de tapis Serge Beaudoin et blessant son compagnon et collègue de travail Jean-Paul Beaumont. Ils croyaient avoir affaire à un contrôle douanier.

Discussion des résultats

Vous avez accès aux codes ayant permis d'avoir ces phrases. Notez que la génération n'a pris pour corpus d'apprentissage seulement les années de Rollin entre 1922 et 2018, c'est-à-dire les années 1938, 1946, 1983, 1987, 2005, 2013, 2015 et 2017. Il eût été visionnaire d'intégrer également les années de Rollin à partir de 1284 pour les raisons historiques, donnant au corpus 70 années supplémentaires pour affiner ses prédictions. Je vous laisse faire l'exercice, il y a juste à changer l'argument à l'appel de rollin.annees_rollin dans main.py.

Autre faiblesse du modèle courant : la méthode RACHE étant ce qu'elle est, quelques erreurs se sont glissées dans le corpus. Rien de grave, mais parfois certains résultats n'apporte pas d'information, voire sont de simples copié-collés d'évènements passés. C'est bien dommage !

Information continue

Bon, c'est pas bien clair, mais on comprend que les années Rollin sont assez violentes, tant en actions militantes qu'en décisions géopolitiques. Ce dont nous avons besoin pour bien comprendre ce monde à venir, c'est d'un programme d'information continue débilitant et abrutissant.

Sur ce, je vous donne une recette magique :

while true; do
    python main.py | shuf -n 1 > out.txt
    cat out.txt
    cat out.txt | espeak -v fr-fr -s 150 &> /dev/null
    sleep 1
done

Cette commande lance le générateur de phrase, en choisi une au hasard qui sera imprimée à l'écran et lue par espeak. Et recommence ad vitam eternam, afin d'assurer un flux d'information continu, comme sur les plus grandes chaînes d'information !

Conclusions & perspectives

La fonction Rollin, définie en quelques minutes par l'éminent professeur éponyme, permet d'associer à une année donnée son nombre de Rollin, entier compris en 1 et 9 inclus. Bien qu'elle n'aie pas été définie suffisemment rigoureusement pour être directement traduite mathématiquement, le professeur a donné suffisemment d'indices qui nous permettent de définir une interprétation possible qui prédit tous les cas donnés par le professeur.

Notre interprétation de la fonction Rollin a ensuite été étudiée, montrant quelques propriétés qu'elle ne possédait pas. C'est fascinant.

Une application évidente de la fonction Rollin a été également implémentée : prédire les évènements des années de Rollin (c'est-à-dire les années dont le nombre de Rollin est le 3) en s'appuyant sur wikipédia pour le corpus d'apprentissage. Bien que des détails doivent encore être étudiés pour améliorer encore cette application, elle prédit déjà des évènements fascinants, tels que l'aide militaire Japonaise pour repousser des partis politiques au Brésil, ou encore des groupes de musique élus présidents.

Les codes étant disponibles librement, il n'est à pas douter que des recherches plus avancées sur la fonction de Rollin et les années du même nom seront entreprises par de nombreuses personnes, la fonction et les années étant source de bien des mystères et comportements rigolos.

Enfin, des mot-clefs tels que machine-learning ou big data ont été ajoutés à la conclusion afin de surfer sur l'hipsterisation du numérique et les facilités de référencement qui vont avec.