Deponia, vous connaissez ? Un point'n click plutôt connu, et que je trouve super sympa.

Ce qui nous intéresse ici, c'est que de temps en temps, il y a ce que le développeur appelle des «mini-jeux», c'est-à-dire des puzzles intégrés dans l'univers, avec leur propre logique, et qui doivent être résolus pour avancer dans le jeu.

L'un d'entre eux m'intéresse particulièrement, car il s'agit d'un excellent exercice de modélisation de problème avec des graphes.

C'est exactement ce que l'on va faire ici : modéliser le problème, et implémenter une méthode pour le résoudre ! (et du coups, ça va donner un spoiler d'une énigme du jeu ; mais rien de grave vu la quantité d'énigmes à résoudre, et qu'il s'agit selon moi de l'une des plus simples du jeu, ne révèlant rien de l'histoire. Donc si vous n'avez pas joué à Deponia, vous ne risquez pas grand chose)

Bon évidemment, le temps de faire les dessins, de faire du code et d'écrire cet article, j'aurais eu le temps de résoudre cette énigme par brute-force plus de 100 fois.

Mais c'est pour la beauté du geste.

prérequis

Théorie des graphes : savoir ce qu'est un graphe orienté est suffisant pour comprendre le modèle.

Pour une introduction à la théorie des graphes, voir ici en vidéo, ou la page wikipédia pour du texte.

Je vais aussi beaucoup utiliser Answer Set Programming (ASP), et plus précisément clingo, l'implémentation de Potassco Labs. Un gros tuto est dispo, mais il n'est pas fondamentalement nécessaire. J'ai énormément annoté les quelques codes, mais l'important, c'est ce qui se passe autour d'eux, pas dedans.

La situation

leviers

Voici la situation :

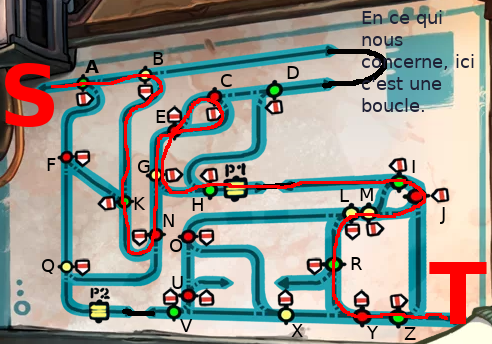
Notre personnage, en bas sur son dragster/chariot des mines (et accompagné d'un autre personnage, plus ou moins en train de faire la sieste), veut passer au travers de la montagne. Les mines sont un véritable dédale, mais heureusement, il y a un plan du réseau de rails !

Le voici en plus gros, où l'on voit les fourches, à chaque fois colorées de vert, rouge ou jaune, et accompagnées d'une flèche qui indique quelle sera la direction empruntée par le chariot. On commence en haut à gauche, on doit aller en bas à droite.

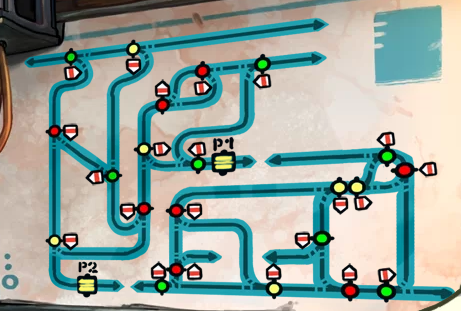
Le joueur peut agir sur trois leviers, un pour chaque couleur, afin de modifier l'aiguillage pour toutes les fourches de ladite couleur. Comme il y a deux chemins possibles pour chaque fourches, le levier a deux positions possibles. La difficulté vient évidemment du fait que l'on change toutes les fourches d'une même couleur à la fois.

portes

Une difficulté supplémentaire vient s'ajouter au problème : les deux portes, notées P1 et P2. Lorsque le chariot passe sur l'une d'elle, les fourches d'une certaine couleur changent d'état. La couleur est fixée à l'aide de boutons situés à côté des leviers, et par défaut, les deux portes sont associées au jaune.

déterminisme

Petit détail important : le jeu est déterministe. Ce que ça veut dire, c'est que si je parcoure la mine deux fois avec la même configuration initiale, je suivrais exactement le même chemin. Ça peut sembler couler de source, mais c'est important de le rappeler.

l'énigme

L'énigme est donc la suivante : sachant que je peux choisir les états initiaux des fourches verte, rouge et jaune, et des deux portes indépendamment, et que ces dernières peuvent changer les états des fourches pendant le calcul de la solution, quelle configuration initiale dois-je choisir pour arriver en bas à droite, i.e à l'autre bout de la mine ?

Arithmétique des configurations

Donc, une configuration, c'est 5 choses :

• l'état de la couleur rouge (1 ou 2)
• l'état de la couleur jaune (1 ou 2)
• l'état de la couleur verte (1 ou 2)
• la couleur de la porte 1 (vert, rouge, ou jaune)
• la couleur de la porte 2 (vert, rouge, ou jaune)

Il est donc possible de compter le nombre de configuration initiales: 2 * 2 * 2 * 3 * 3 = 8 * 9 = 72

Déjà, on peut remarquer quelque chose d'important : c'est peu. À raison d'une vingtaine de secondes pour tester une solution un peu longue (où le chariot fait beaucoup de détours), il faut moins d'une demi-heure pour brute-forcer le problème.

description d'une configuration

Mettons nous tout de suite d'accord pour nous simplifier la vie plus tard. Pour représenter une configuration, j'écrirais par exemple 122JR, pour dire que les fourches rouge sont à 1, les jaune à 2, les verte à 2, P1 est colorée en jaune, et P2 est colorée en rouge.

Et lorsque les couleurs des portes n'auront pas d'importance, j'écrirais juste les trois premiers chiffre.

La configuration montrée dans les captures d'écran du jeu est 111JJ, c'est la configuration initiale dans le jeu. Le joueur est libre de modifier cette configuration à l'aide de différents boutons, puis de la tester, puis de recommencer, jusqu'à réussite. Il ne peut pas la modifier pendant le parcours des mines, donc le joueur n'a aucun pouvoir sinon celui de choisir la configuration initiale.

Modélisation simple

La théorie des graphes, c'est génial [[citation needed]], et pour ce problème précis, c'est parfaitement adapté.

Tout d'abord, donnons des noms aux fourches (on garde P1 et P2 pour les deux portes), et au départ et à l'arrivée:

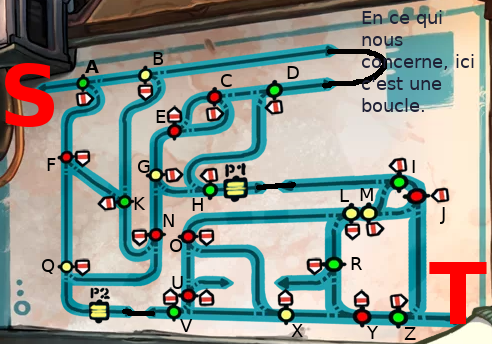
Maintenant, nous pouvons observer une propriété intéressante du graphe : si je prend par exemple la fourche A, et je dis que j'arrive dessus par la gauche (donc en position de choix). Question : où vais-je aller ensuite ? La réponse peut-être répondue partiellement par : si les fourches vertes (donc A) sont dans l'état 1 (l'état montré par l'image plus haut), alors le chariot va rejoindre la fourche B, et ce qui arrivera ensuite sera totalement dicté par celle-ci. Si en revanche les fourches vertes sont dans l'état 2, le chariot va descendre et rejoindre la fourche F. Et comme pour B, le reste du voyage ne sera plus décidé que par F et la configuration.

Bref, ce qui est à retenir ici, c'est que l'exploration du plan est déterministe et surtout ne dépends que de deux choses : la prochaine fourche rencontrée, et la configuration.

(Notons que lorsqu'une fourche est prise «à l'envers», par exemple la fourche C quand le chariot arrive de D, elle n'a pas d'influence sur le déplacement. Dans le cas précis d'un chariot qui partirais de D en direction de C, la prochaine fourche qu'il rencontrera et qui déterminera la suite du chemin sera la fourche G)

Modélisation avec un graphe orienté

Fort de cette considération, nous pouvons modéliser le plan comme un graphe, où :

• les sommets sont les fourches du plan.
• les arcs relient une fourche à la fourche suivante.

Par exemple, dans notre graphe, le nœud A, symbolisant la fourche A, sera relié à deux autres nœuds, B et F.

On ajoute également deux nœuds spéciaux : l'entrée (S, pour start), et la sortie (T, pour terminal). Afin de conserver l'information du choix dirigé par la couleur, nous allons également :

• garder les couleurs sur les nœud. Ainsi le nœud A est vert, car la fourche A est verte.
• valuer les arcs avec les valeurs 1 ou 2. Chaque nœud possèdera alors deux arcs sortants, un libellé «1», qui pointera vers le nœud suivant lorsque la configuration indique «1» pour la couleur du nœud, et «2», qui sera l'autre état. Par exemple, l'arc allant de A à B sera valué 1, car par défaut la fourche A mène à la fourche B, et celui allant de A à F sera libellé d'un «2».

Notez qu'avec cette solution, nous n'avons pas besoin de réfléchir au sens dans lequel une fourche est rencontrée : en fait, une fourche prise «à l'envers» est ignorée dans le modèle. Nous perdons une information, mais une information inutile : ce qui nous intéresse c'est le parcours, pas la liste des fourches croisées.

Gestion des portes

Les portes complexifient un poil le modèle. La solution naïve consiste à faire un nœud pour chacune. Mais ça ne marche pas, puisque leur fonctionnement est asymmétrique, contrairement aux nœuds du graphe. Effectivement, si je vous dit «j'arrive sur P1, je vais où après ?», vous ne pouvez pas me répondre, car il y a deux possibilités : H ou J. Et ça dépends d'où je viens.

Avec la solution naïve, on doit s'obliger à se souvenir d'où on vient, et de permettre à un nœud d'agir selon cette nouvelle information. Pas pratique, et même carrément moche si vous voulez mon avis.

La solution très standard à ce genre de problème, c'est d'avoir pour une porte, non pas un, mais DEUX nœuds.

Par exemple, pour la porte P1, appellons les deux nœuds P1G (G pour gauche) et P1D (D pour droite). Maintenant, on énonce la propriété suivante :

• lorsqu'une fourche débouche sur P1 par la droite, le nœud associé sera relié à P1D.
• vice-versa avec gauche et P1G.
• on relie P1D avec la fourche rencontrée lorsque l'on sort par la gauche de la porte, avec un arc libellé de «1» et «2», car une porte n'a qu'une seule destination dans un sens donné.
• vice-versa pour P1G.

Avec cette solution, tout d'un coups, tout devient simple : on va mettre un arc libellé de «1» et «2» qui ira de P1D à H, car lorsqu'on rentre dans P1 par la droite, on arrive forcément sur H juste après. De la même manière, toutes les fourches envoyant sur le côté gauche de P2 (donc juste Q dans ce cas-là) seront reliés à P2G. Et P2G sera relié à V, la fourche que l'on rencontre lorsqu'on sort de P2 après y être arrivé par la gauche.

Notons cependant que cela ne gère pas l'effet de bord des portes : elles changent la configuration. Ceci n'est pas géré par notre modèle, mais nous verrons comment régler ce problème… petit à petit.

Exemple de rendu final

Voici un exemple avec juste les arcs partant de A, B, D et F :

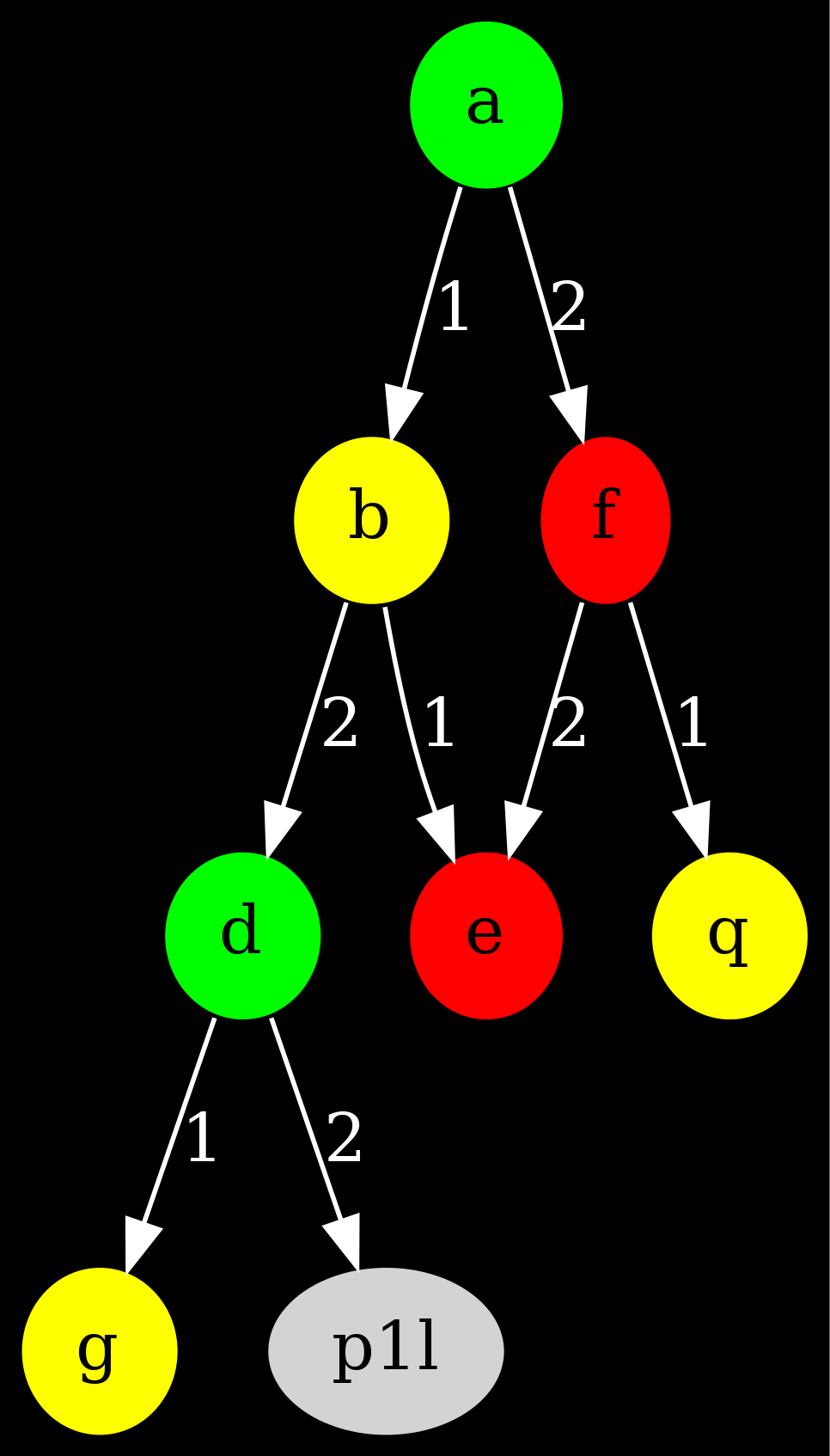
Allez-y, vérifiez en regardant sur le plan. Mais du coups, est-ce qu'on aura le vrai graphe ? Bien sûr, mais d'abord il faut… le récupérer.

Récupération des données
(et pause père castor)

Ça, c'est la partie chiante (du moins pour moi) : récupérer et encoder le graphe qui correspond au plan du jeu.

Notez que j'aurais pu en générer un moi-même, et l'utiliser à la place du plan du jeu. Ça m'aurait évité une demi-heure d'arrachage d'yeux sur une capture d'écran annotée (demi-heure que j'aurais pu utiliser pour brute-forcer l'énigme, au passage).

Mais voyez-vous, l'instance du jeu à un intérêt tout particuliers : elle a été pensée pour être intéressante.

Et oui. Si je génère un graphe sans plus y travailler. Il est très probable qu'il n'y ait pas de solution. Ou qu'elle soit triviale. Ou trop dure à trouver (parce que tant qu'à y être, on génère un graphe avec 1 millions d'arcs, comme ça c'est sûr, la durée de vie du jeu va augmenter considérablement).

Anecdote intéressante : le développeur (dont les commentaires sont accessibles dans le jeu) explique justement lorsqu'il parle de cette énigme qu'un bug horrible faisait que dans certains cas… le chariot ne s'arrêtait jamais. Il rentrait dans un cycle. Sur un graphe généré aléatoirement, ce genre de problème est très probable : il suffit que arriver sur une fourche avec une certaine configuration mène à un moment ou à un autre, sur cette même fourche avec la même configuration. Le développeur raconte ensuite qu'il a passé beaucoup de temps et de crise de nerf à corriger le plan, jusqu'à être sûr à 100% qu'il n'y ait aucun cycle. Et que l'énigme soit toujours intéressante. Et pas trop complexe non plus.

Bref, dans cet article, on va regarder comment ledit développeur aurait pu modéliser le problème, et faire une exploration automatique de l'espace des solutions, et donc trouver les problème de cycles, et les bonnes solutions s'il y en a (parce que oui, sans vouloir spoiler, c'est exactement ce qu'on va faire).

Données brutes

Bref, une demi-heure de fun absolu, une autre demi-heure de vérification, et voilà ! J'ai extrait à la main (j'aurais bien fait une détection automatique avec de l'OCR ou des réseaux de neurones, mais ça fait beaucoup (et surtout un autre article) et j'ai que deux jours par weekend) les informations importantes qui permettent de faire le graphe.

En gros, je les ai extraites en ASP (fichier complet ici), parce que c'est avec ce language qu'on va jouer dans cet article, et ça donne des lignes comme ça :

nodecolor(c,rouge).  % la fourche C est rouge
rel(c,1,s).   % par défaut, de C on retourne au début :(
rel(c,2,g).   % et sinon, on va sur G
rel(d,1,g).   % par défaut, de D on va à G
rel(d,2,p1l). % sinon, de D on entre dans porte 1 par la gauche

Il y a d'autres infos assez standards, comme les couleurs des nœuds, le nœud de départ S, le nœuds de sortie T,… Bref, tout ce qui définit cette instance du problème !

Avec biseau, on peut afficher le graphe en utilisant ça:

color((a;d;h;i;k;r;v;z),green).
color((b;g;l;m;q;x),yellow).
color((c;e;f;j;n;o;u;y),red).

link(X,Y):- rel(X,_,Y).
dot_property(X,Y,taillabel,L):- rel(X,L,Y).

obj_property(edge,arrow_head,vee).
obj_property(edge,color,white).
obj_property(edge,fontcolor,white).
obj_property(graph,bgcolor,black).
obj_property(graph,dpi,400).

Et on obtient le graphe qui modélise l'instance, tel que définit plus haut, que j'ai nommé le graphe Deponia :

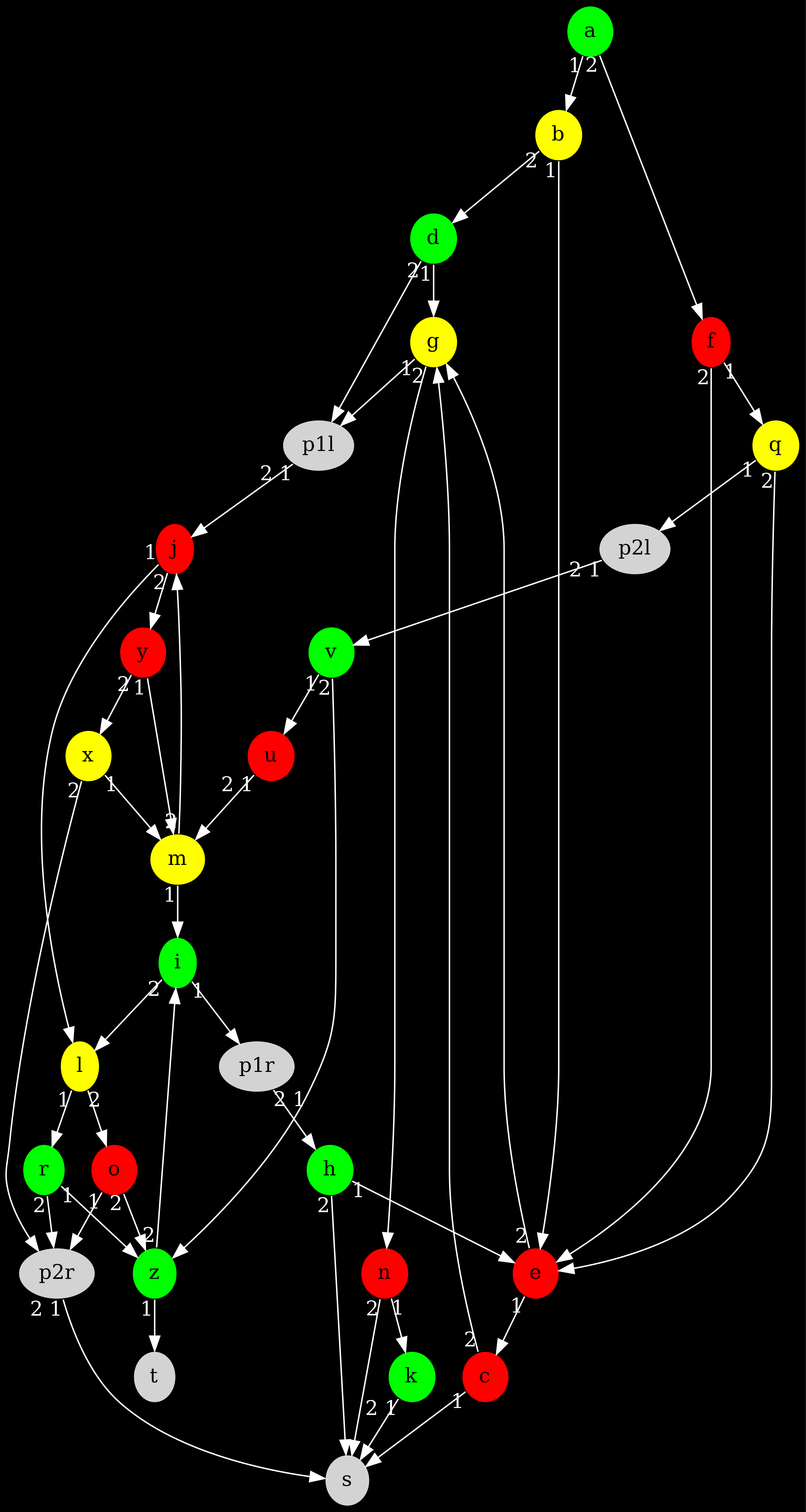
Et ça veut dire qu'il manque pas grand chose pour commencer à faire des trucs… C'est parti !

Résolution sans portes

Le problème des portes, comme nous l'avons vu, n'est que partiellement résolu : elles changent la configuration. C'est nul. Bou. Mauvais.

Bon, en réalité il y a plusieurs manières de les gérer. Mais avant, on peut se poser la question : existe-t-il une solution qui ne passe pas par une porte ?

Et la réponse, on peut facilement la déterminer avec ASP:

% Recherche d'une solution sans passer par les portes !

% On choisi une valeur pour une couleur donnée:
1{colorvalue(C,1..2)}1:- nodecolor(_,C).
rjv(R,J,V):- colorvalue(rouge,R) ; colorvalue(jaune,J) ; colorvalue(vert,V).

% Le path nous permettra de suivre le déplacement.
%  On commence au nœud de départ (logique).
path(1,Noeud):- start(Noeud).
% On arrive au nœud succédant au dernier path, selon les valeurs de couleur.
path(N,Succ):- path(N-1,Pred) ; rel(Pred,ColorVal,Succ) ; nodecolor(Pred,Color) ; colorvalue(Color,ColorVal).
% Cas spécial: les portes n'ont pas de couleur.
% path(N,Succ):- path(N-1,Pred) ; rel(Pred,_,Succ) ; not nodecolor(Pred,_).  % on désactive, car on gère pas encore les portes

% État de la réponse: soit on a trouvé (win), soit on est retourné au départ (loss).
game(win,N):- path(N,t).
game(loss,N):- path(N,s).
% Cas spécial dû à notre contrainte sur les portes: on peut être n'importe où.
game(lost,(N,E)):- path(N,E) ; not path(N+1,_) ; not final_node(E).

#show.
#show rjv/3.
#show path/2.
#show game/2.

Même si vous ne connaissez pas ASP, vous pouvez faire tourner le code sur le net, mais le mieux ça reste de télécharger le binaire, et de lui donner les fichiers à manger, par exemple avec clingo graph.lp no-porte.lp -n 0 (le -n 0, c'est pour avoir toutes les solutions).

Quoiqu'il en soit, voici la sortie du solveur :

Answer: 1
path(1,a) rjv(1,1,2) path(2,f) path(3,q) path(4,p2l) game(lost,(4,p2l))
Answer: 2
path(1,a) rjv(2,1,2) path(2,f) path(3,e) path(4,g) path(5,p1l) game(lost,(5,p1l))
Answer: 3
path(1,a) rjv(2,1,1) path(2,b) path(3,e) path(4,g) path(5,p1l) game(lost,(5,p1l))
Answer: 4
path(1,a) rjv(1,1,1) path(2,b) path(3,e) path(4,c) path(5,s) game(loss,5)
Answer: 5
path(1,a) rjv(2,2,1) path(2,b) path(3,d) path(4,g) path(5,n) path(6,s) game(loss,6)
Answer: 6
path(1,a) rjv(2,2,2) path(2,f) path(3,e) path(4,g) path(5,n) path(6,s) game(loss,6)
Answer: 7
path(1,a) rjv(1,2,2) path(2,f) path(3,q) path(4,e) path(5,c) path(6,s) game(loss,6)
Answer: 8
path(1,a) rjv(1,2,1) path(2,b) path(3,d) path(4,g) path(5,n) path(6,s) game(loss,6)
SATISFIABLE

Models       : 8
Calls        : 1
Time         : 0.001s (Solving: 0.00s 1st Model: 0.00s Unsat: 0.00s)
CPU Time     : 0.000s

On voit 8 réponses, numérotée de 1 à 8. Ça colle avec nos attentes : il y a bien 8 combinaisons de configuration dans notre cas (2 états possibles pour 3 couleurs). La configuration est donnée par l'atome rjv/3. Par exemple, dans la première réponse, rjv(1,1,2) indique que le vert est fixé à 1, le jaune à 1 et le rouge à 2.

Maintenant, en regardant on comprend le sens des autres atomes :

• path(N,F): à l'étape N, on est sur la fourche F. On voit qu'on commence toujours à a à l'étape 1, et qu'ensuite on va soit vers f, soit vers b, selon la valeur assignée au fourches vertes.
• game(lost,(N,F)): on est perdu ou bloqué à l'étape N, à la fourche F. Ceci n'est pas possible dans l'énigme, mais comme nous ne gérons pas encore les portes, c'est possible. Notez qu'à chaque fois la fourche d'arrêt est une porte.
• game(loss,N): à la N-ième étape, on est arrivé sur le nœud S (start). Ça veut dire qu'on a perdu.
• game(win,N): à la N-ième étape, on est arrivé sur le nœud T (terminal). Ça veut dire qu'on a gagné. Et non, aucun answer set ici n'y arrive.

Voilà, avec ça nous avons plusieurs informations :

• d'abord, on est obligé de passer par les portes pour trouver la sortie
• les configurations 111, 221, 222, 122, et 121 sont des peines perdues : pas besoin de gérer les portes pour voir qu'elles n'arriveront jamais à donner de bonne solutions, puisqu'elles retournent à la case départ avant même d'en avoir vu une.

Voilà, juste avec quelques lignes de code, nous venons de réduire l'espace de recherce. Il n'y a plus 72 configurations à explorer, mais juste… 27.

Anecdote : la configuration 111 est à la fois la configuration de départ dans le jeu, et celle qui se termine en un minimal d'étape. Coìncidence ?

Modélisation complète avec état dynamique

Bon, on a compris : sans les portes, c'est nul. Quelle idée aussi d'implémenter l'énigme qu'à moitié !

Pour gérer les portes, une solution simple consiste à considérer les états des fourches comme dynamiques, c'est-à-dire changeant à la manière du numéro d'étape (le premier argument de path/2). Voici donc dy-porte.lp, une implémentation qui utilise les atomes path/3 pour encoder les chemins (ça commence à être de l'ASP un peu velu):

% Recherche d'une solution avec les couleurs en état dynamique !

% Pour éviter de tourner ad vitam eternam en cas de cycle, on s'impose une limite
#const path_maxlen=100.  % 100, c'est LARGEMENT suffisant sur cette instance

% On choisi une valeur pour une couleur donnée.
1{colorvalue(C,1..2)}1:- color(_,C).
rjv(R,J,V):- colorvalue(rouge,R) ; colorvalue(jaune,J) ; colorvalue(vert,V).
% On choisi une couleur pour chaque porte.
1{gatecolor(Num,(rouge;jaune;vert))}1:- gate(Num,_).

% Le path nous permettra de suivre le déplacement.
%  On commence au nœud de départ, avec la configuration de départ (logique).
path(1,Noeud,rjv(R,J,V)):- start(Noeud) ; rjv(R,J,V).
% On arrive au nœud succédant au dernier path, selon les valeurs de couleur.
path(N,Succ,RJV):- path(N-1,Pred,RJV) ; rel(Pred,ColorVal,Succ) ; color(Pred,Color) ; define_colorvalue(Color,RJV,ColorVal) ; N<path_maxlen.
% Cas spécial: les portes n'ont pas de couleur.
path(N,Succ,rjv(R2,J2,V2)):-
    path(N-1,Pred,rjv(R,J,V)) ; rel(Pred,_,Succ) ; N<path_maxlen ;
    gate(NumGate,Pred) ;  % on s'apprête à quitter une porte
    gatecolor(NumGate,GateColor) ;  % on s'apprête à changer une couleur
    define_state(rouge,GateColor,R,R2) ;  % on détermine la nouvelle valeur de RJV.
    define_state(jaune,GateColor,J,J2) ;
    define_state(vert,GateColor,V,V2).

% Partie un peu difficile : il faut définir le nouvel état (arg 4) d'une couleur (arg 1), sachant la couleur d'une porte traversée (arg 2), et son état actuel (arg 3).
define_state(Color,Color,State,New):-  % la couleur considérée est la même que la porte : la valeur doit changer !
    color(_,Color) ; State=1..2 ; New=3-State.
define_state(Color,OtherColor,State,State):-  % couleur différente de la porte : on laisse en l'état
    color(_,Color) ; color(_,OtherColor) ; Color!=OtherColor ; State=1..2.

% De la même manière, il faut définir la valeur d'état à prendre en compte (arg 3), sachant la couleur d'une fourche (arg 1) et la config actuel (arg 2).
define_colorvalue(rouge,rjv(R,J,V),R):- R=1..2 ; J=1..2 ; V=1..2.
define_colorvalue(jaune,rjv(R,J,V),J):- R=1..2 ; J=1..2 ; V=1..2.
define_colorvalue(vert,rjv(R,J,V),V):- R=1..2 ; J=1..2 ; V=1..2.

% État de la réponse: soit on a trouvé (win), soit on est retourné au départ (loss).
game(win,N):- path(N,t,_).
game(loss,N):- path(N,s,_).
game(cycle,N):- path(N,E,_) ; not path(N+1,_) ; not final_node(E).

% On vire les cas qui nous intéressent pas, c'est-à-dire ceux où on perd.
%  (les cycles nous intéressent, car ils montrent un problème dans l'instance)
:- game(loss,_).

#show.
#show rjv/3.
#show path/3.
#show game/2.
#show gatecolor/2.

Un programme plus complexe, car il nécessite un traitement un peu délicat pour le nouvel argument de path/3. Pour les fourches, il faut être capable de déterminer quel chemin prendre en fonction non pas de la configuration initiale, mais de la configuration courante. De la même manière, pour les portes, il faut définir le nouvel état d'une couleur, sachant la couleur d'une porte traversée, et l'état actuel de ladite couleur.

Notez également la présence d'une constante path_maxlen, qui permet de réagir en cas de cycle impromptu.

Et, bien sûr, voilà le résultat proposé par le solveur !

Answer: 1
rjv(2,1,1) path(1,a,rjv(2,1,1)) path(2,b,rjv(2,1,1)) path(3,e,rjv(2,1,1)) path(4,g,rjv(2,1,1)) gatecolor(2,rouge) path(5,p1l,rjv(2,1,1)) gatecolor(1,rouge) path(6,j,rjv(1,1,1)) path(7,l,rjv(1,1,1)) path(8,r,rjv(1,1,1)) path(9,z,rjv(1,1,1)) path(10,t,rjv(1,1,1)) game(win,10)
Answer: 2
rjv(2,1,1) path(1,a,rjv(2,1,1)) path(2,b,rjv(2,1,1)) path(3,e,rjv(2,1,1)) path(4,g,rjv(2,1,1)) gatecolor(2,vert) path(5,p1l,rjv(2,1,1)) gatecolor(1,rouge) path(6,j,rjv(1,1,1)) path(7,l,rjv(1,1,1)) path(8,r,rjv(1,1,1)) path(9,z,rjv(1,1,1)) path(10,t,rjv(1,1,1)) game(win,10)
Answer: 3
rjv(2,1,1) path(1,a,rjv(2,1,1)) path(2,b,rjv(2,1,1)) path(3,e,rjv(2,1,1)) path(4,g,rjv(2,1,1)) gatecolor(2,jaune) path(5,p1l,rjv(2,1,1)) gatecolor(1,rouge) path(6,j,rjv(1,1,1)) path(7,l,rjv(1,1,1)) path(8,r,rjv(1,1,1)) path(9,z,rjv(1,1,1)) path(10,t,rjv(1,1,1)) game(win,10)
Answer: 4
rjv(1,1,2) path(1,a,rjv(1,1,2)) path(2,f,rjv(1,1,2)) path(3,q,rjv(1,1,2)) path(4,p2l,rjv(1,1,2)) path(5,v,rjv(1,1,1)) gatecolor(2,vert) gatecolor(1,rouge) path(6,u,rjv(1,1,1)) path(7,m,rjv(1,1,1)) path(8,i,rjv(1,1,1)) path(9,p1r,rjv(1,1,1)) path(10,h,rjv(2,1,1)) path(11,e,rjv(2,1,1)) path(12,g,rjv(2,1,1)) path(13,p1l,rjv(2,1,1)) path(14,j,rjv(1,1,1)) path(15,l,rjv(1,1,1)) path(16,r,rjv(1,1,1)) path(17,z,rjv(1,1,1)) path(18,t,rjv(1,1,1)) game(win,18)
SATISFIABLE

Models       : 4
Calls        : 1
Time         : 0.002s (Solving: 0.00s 1st Model: 0.00s Unsat: 0.00s)
CPU Time     : 0.003s

Quatre ! Il y a quatre bonnes réponses possibles selon notre programme ! Ah, c'est beau, je suis tellement pressé de les tester !

Tiens, en attendant, voilà le tracé sur le plan de la première !

Quelques observations en vrac avant de couper avec une transition grave et sérieuse :

• si vous virez la contrainte qui empêche les réponses qui trouvent un chemin qui retourne au début, vous obtiendrez exactement 72 réponses. C'est beau les maths.
• il n'y a que des mauvaises ou des bonnes réponses. Pas de cycle qui coince le joueur. Le développeur a bien fait son job !
• le temps de calcul pour ce problème est dérisoire. Quand on connait bien ASP, ce genre de programme s'écrit et se debug en quelques dizaines de minutes. Bref, ASP c'est un super language pour les prototypes, et au-delà.
• on se trimballe quand même avec un état supplémentaire (le RJV), qu'on modifie lorsqu'on passe une porte. C'est chiant, c'est moche, et c'est pas un graphe. Moi j'aime les graphes.

Relisez bien cette dernière phrase, parce qu'elle motive toute la dernière partie : avec notre état dynamique, on gère bien la crise, sans trop se prendre la tête, et de manière assez efficace. Mais les graphes, c'est tellement beau qu'on en met partout.

Modélisation complète avec expansion du graphe

Est-il possible de modéliser complètement le problème avec uniquement un graphe orienté ? Sans état global modifié durant l'exécution ? Sans état global tout court ? OUI !

La solution est en fait assez standard.

intuition

Réfléchissons. Si on considère une instance où il n'y a pas de portes, ça veut dire que la configuration ne peut pas changer. Autrement dit, on ne pourra, connaissant une configuration, pas passer par certains arcs. Par exemple, si la configuration initiale fixe le vert à l'état 1, alors on pourrait enlever tous les arcs libellés d'un «2» qui lient un nœud vert vers un autre nœud.

En fait, on pourrait, plutôt qu'un seul graphe avec tous les arcs, avoir un graphe pour chaque configuration, avec uniquement les arrêtes que l'on peut emprunter. Par exemple, le graphe pour la configuration 111 aurait le lien de A vers B, mais pas celui de A vers F. À l'inverse des graphes pour les configurations 112, 122, 212, et 222.

Les conséquences sont intéressantes :

• on génère 8 graphes, un pour chaque configuration.
• il n'y a plus qu'un arc sortant par nœud, puisque la configuration ne change pas.
• donc plus besoin de labelliser les arcs.
• il y a donc un point de départ pour chaque configuration, et plutôt que choisir une configuration, on choisit un point de départ.
• trouver les solutions revient à trouver les points de départs qui sont liés à la sortie.

Juste, le fait qu'une fois arrivé sur un nœud, on ait qu'un seul et unique choix… C'est bouleversant !

Voici par exemple le graphe expansé pour la configuration 111, avec uniquement les nœuds atteignables depuis le départ ou une porte :

Idem pour la configuration 211:

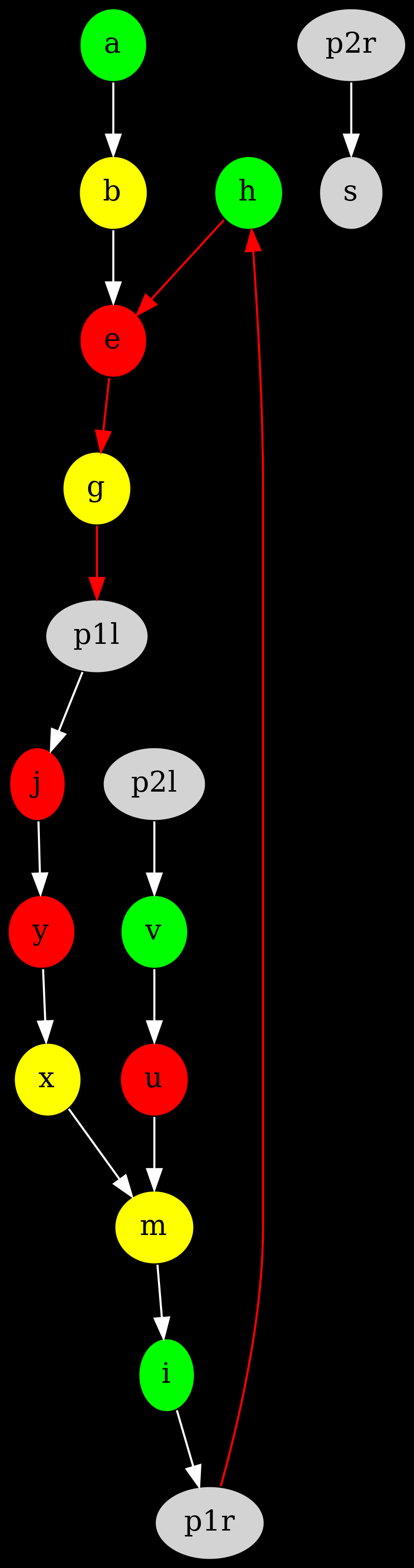
Bon, ok, mais nous ne gèrons pas les portes. Et elles commencent à nous ennuyer avec leur changement de configuration. Sauf que, nous allons le voir, notre modèle de graphe expansé fonctionne très bien. Il nous faut juste 66 graphes supplémentaires.

Open the gate

Une porte, ça change de configuration. Hors, on vient de voir qu'on pouvait avoir un graphe pour chaque configuration. Donc, si on change de configuration… on change de graphe !

C'est comme si les graphes étaient des planètes différentes, et les portes des Portes des Étoiles que le chariot peut emprunter pour sauter d'une planète à l'autre.

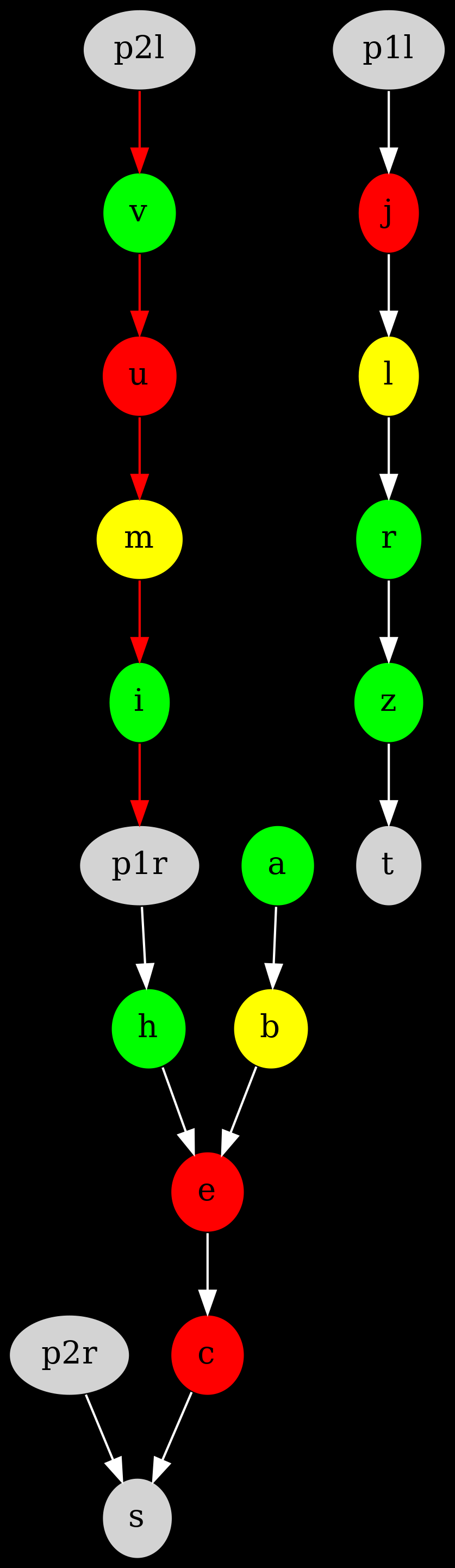
Pour l'exemple, voici le cheminement de la quatrième solution trouvée dans la partie précédente :

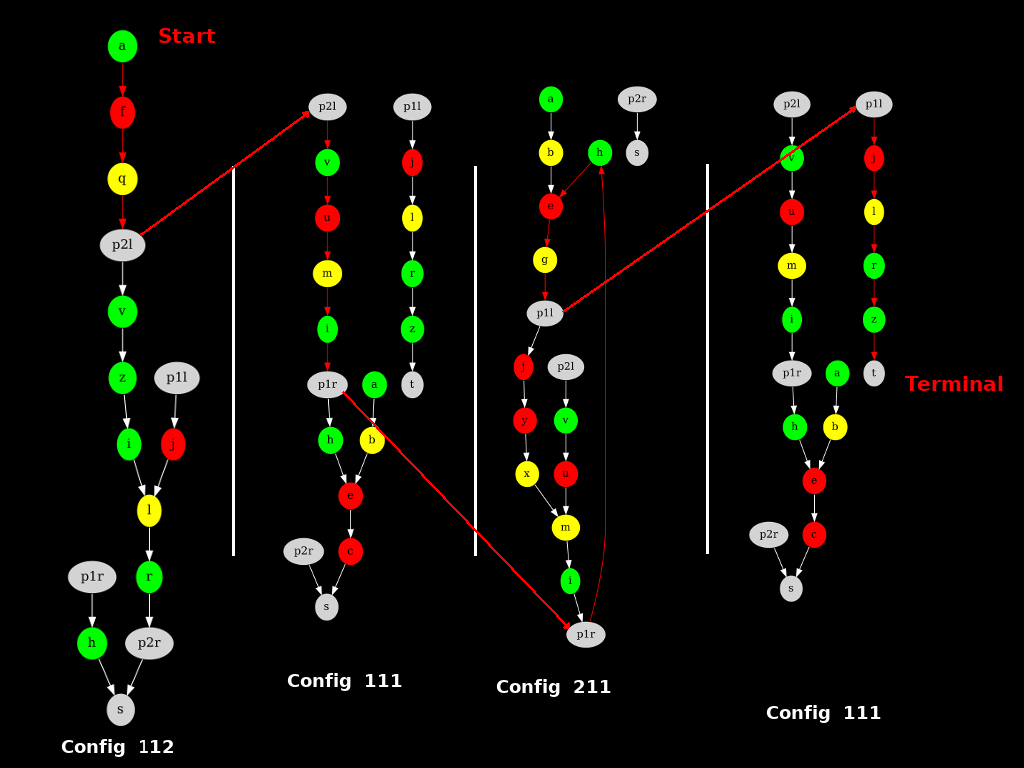
On commence à la fourche A dans la configuration 111, et on termine à T dans la configuration 112. Entre temps, comme le montre le chemin coloré en rouge et la solution données par ASP, on saute d'un graphe à l'autre via les Portes des Étoiles. Finalement, on ne rencontre jamais de choix, mais on passe à travers les configurations 112 (celle initiale), 111, 211 et encore 111.

Notez cependant qu'ici, on n'a que 4 des 72 configurations. Le graphe expansé est en réalité beaucoup plus grand.

Hold the gate

Cette méthode est géniale : il n'y a plus qu'un graphe orienté à gérer, et notre problème se réduit à chercher un chemin entre les starts et le terminal !

Mieux ! Vous vous souvenez de ce jeu dans les magazines de coloriage pour enfants ? Où il faut trouver un chemin parmis plusieurs qui arrive jusqu'à un objectif (un exemple là).

La technique que tout le monde applique très vite, c'est, plutôt que d'essayer chaque chemin individuellement jusqu'à trouver le bon (c'est du brute-force), de commencer par la fin… et de remonter jusqu'au début du chemin qui est, de facto, le bon.

Eh bien, nous aussi, nous pouvons appliquer cette astuce millénaire : inversons les arcs du graphe (A->B devient B->A), et partons du nœud terminal. Maintenant, tout ce que nous avons à faire, c'est un bête parcours de graphe (un simple DFS fera le job, mais Dijkstra permet de récupérer le nombre d'étape) pour énumérer les nœuds que nous rencontrons, et plus particulièrement ceux qui nous intéresse, c'est-à-dire les entrées.

Ainsi, il y aura deux types d'entrées (et donc de configurations, puisque chacune des 72 configurations possède son entrée) : celles qu'on va trouver pendant le parcours, et celles qu'on ne trouvera pas. Les premières sont les bonnes configurations qui permettent de répondre au problème initial : passer au chapitre suivant de Deponia.

Le graphe unique qui contient toutes les configurations est gigantesque. J'ai pas réussi à le générer avec dot. Du coups, voilà une image du graphe Deponia compressé pour compenser :

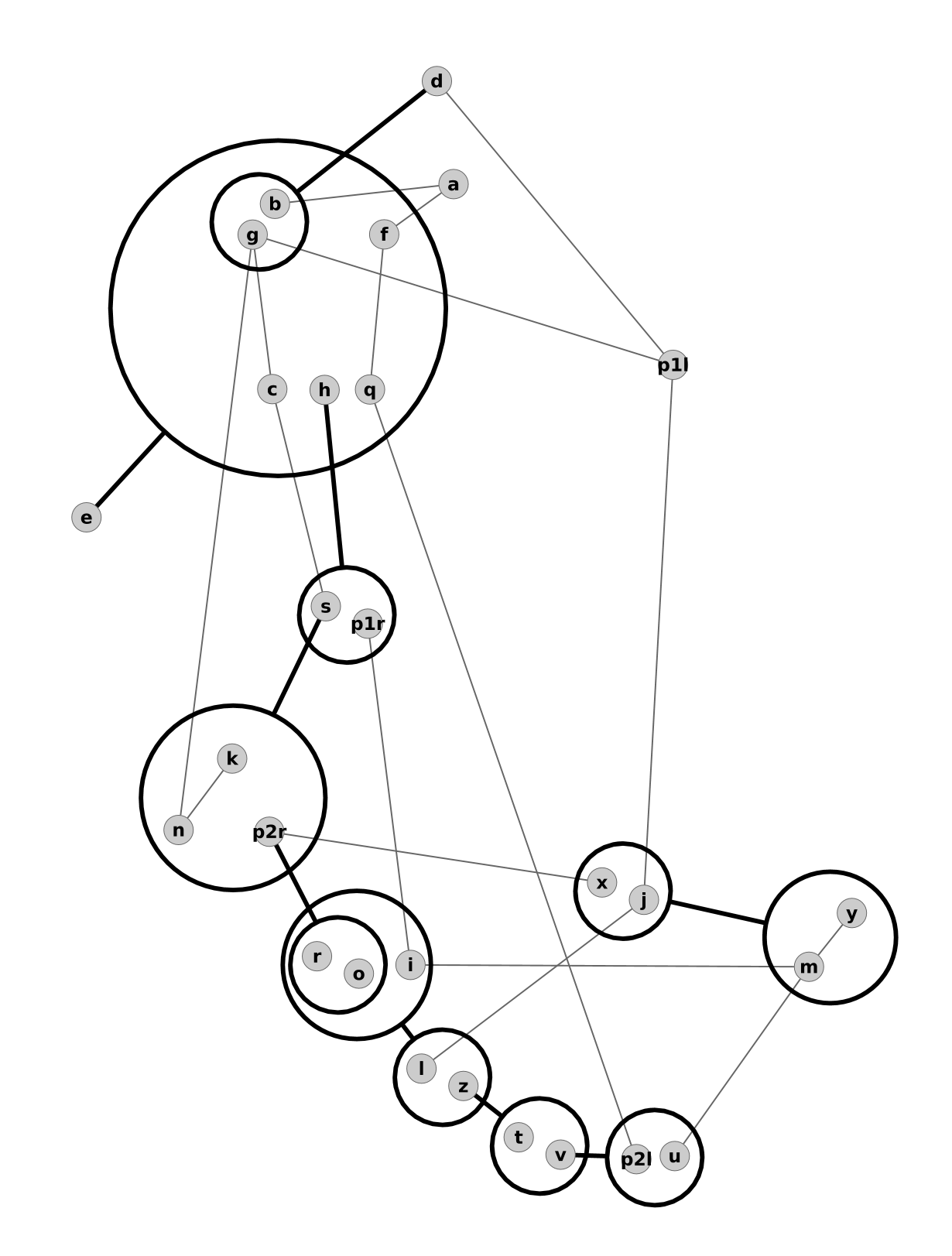
Close the gate

Cette approche, quoique majestueuse (parce que, pour le coups, il ne reste plus qu'un unique graphe), possède néanmoins un inconvénient majeur. C'est lourd. Avec la première méthode, on se coltine juste un état global, pas spécialement coûteux en mémoire, et aujourd'hui les ordinateurs sont suffisemment puissants pour gérer le léger coût CPU que la méthode implique.

Mais avec le graphe unique et les Portes des Étoiles, tout de suite ça commence à exploser en mémoire. Rajoutez une porte, vous passez de 72 configurations à 216. Rajoutez-en encore une, et vous arrivez à 648 graphes imbriqués. À 26 arcs par graphes, c'est un total de 16 848 arcs qu'il va falloir gérer. Juste pour 24 nœuds et 52 arcs dans le problème de base.

Bref, le machin grossit en mémoire de manière exponentielle. Ça peut être gênant.

Restons néanmoins positifs : nous avons un graphe qui gère tout. Tout seul. Ya même plus de cas particulier pour les portes !

Conclusions

Quels avantages à modéliser ?

Pour l'instance seule, donc c'est-à-dire ce puzzle précis de Deponia, on se demande bien l'intérêt.

Sauf que maintenant, si jamais dans le futur on croise une autre instance de ce problème, nous pourrons ressortir toute la quincaillerie, et utiliser des algos standards pour la résoudre. Après tout, nous venons de réduire l'énigme du jeu à un parcours de graphe.

D'autant qu'un gère :

• n'importe quel réseau minier
• n'importe quel nombre de porte (y compris les Porte des Étoiles)
• n'importe quel jeu de couleur
• des fourches de 2 choix ou plus (il suffit d'introduire un label «3» pour gérer les fourches à trois branches, par exemple)
• les sorties multiples, les points de départs multiples
• la détection automatique des solutions, des configurations non-valides ou bloquantes (celles qui débouchent sur un cycle)

Et tout ça avec de jolis graphes. C'est bô.

Coût

Ce projet a tenu sur la durée parce que c'était essentiellement de l'écriture d'article. Les codes ont été écris en 1h, j'ai passé plus de temps à faire les images (et sans biseau j'y serais encore).

Perspectives

En soit, on a fait le tour du problème, mais il reste quelques questions en suspend.

Implémentation au propre

C'est un peu beaucoup pour la seule instance trouvée dans Deponia, mais si vous êtes un fan de ce genre de puzzle… Vous avez le code ASP, et clingo peut être intégré à du C, du lua ou du python. Même pas besoin de refaire vous-même les algos.

Bref, un truc assez simple à faire, ce serait une implémentation propre avec des formats d'entrée standard pour décrire l'instance à résoudre, et une interface qui donne les infos avec un beau formatage facile à lire pour un humain. Un programe qui pourrait aussi faire de la génération de puzzle :

Génération de puzzles

Est-il possible de construire un programme qui génèrerait des puzzles ? En soi, oui : génèrer un graphe aléatoirement, avec les propriétés qui m'intéressent concernant les degrés sortants des nœuds, et faire tourner les codes vus dans cet article pour déterminer si :

• il y a au moins une solution (au moins une réponse avec «win»)
• il y a pas trop de solution (pas plus de quelques réponses avec «win»)
• il n'y a aucun cycle atteignable (pas de réponse avec «cycle»)

Et recommencer jusqu'à trouver un graphe «intéressant». Le problème de cette approche, c'est que nous ne savons pas combien de temps il va falloir avant de génerer un graphe intéressant. Probablement longtemps.

La solution : être capable de transformer un graphe inintéressant en graphe intéressant. Le truc vital, c'est déjà d'être capable de modifier le graphe généré pour virer les cycles. Ça peut se faire de manière heuristique, mais encore une fois, sans garantie de performance.

Peut-être est-il possible de formaliser exactement les propriétés d'un graphe «intéressant», ou en tout cas d'un sous-ensemble ? Ce serait sympa d'y réfléchir, car il y a de l'auto génération de puzzle à la clef.

Autres puzzles

Il y a bien d'autres puzzles dans Deponia, ainsi que dans d'autres jeux. Bien des tâches peuvent être abstraites et traitées formellement ainsi. Celui-ci était assez évident : dans le jeu même, on voit un graphe dessiné.

C'est un exercice intéressant et rigolo que d'attaquer les jeux de manière mathématique. Le premier exemple qui me vient à l'esprit, c'est les pokésciences, où l'on va jusqu'à étudier l'influence d'un opposant particulier sur l'évolution des stats d'un pokémon, ainsi que le système de combat très bien formalisé. L'autre exemple typique, c'est EVE online, où les joueurs les plus assidus du côté économique/ressource travaillent sur des tableurs complexes pour gérer leurs productions (la communauté est connue pour ce côté «simulateur de tableur dans l'espace»).

Sans surprise, la durée de vie des jeux (et l'intérêt qu'on peut y porter) augmente beaucoup avec ce genre d'approche.

mot de la fin

J'ai passé 12h non-stop sur une énigme de Deponia, plus 6 autres heures pour fignoler et traduire.

Sur ce, je vous laisse, je vais configurer mon dragster des mines.